Kronecker's dalta (definition and application examples)
Kronecker's delta is a function on $i, j = 1,2, \cdots, n$ defined as
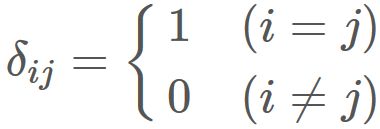
Examples (n=3)
The definition of Kronecker's delta is
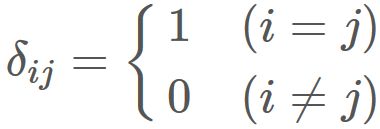
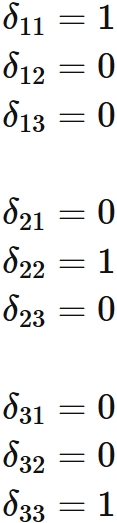
Identity matrix
Let $A$ be the matrix whose elements are Kronecker's delta.
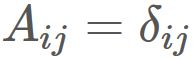
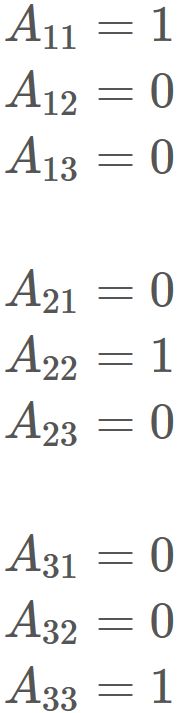
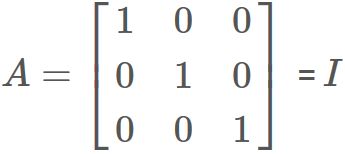
Let $\mathbf{a}$ be an arbitrary three-dimensional vector,
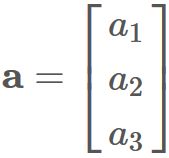
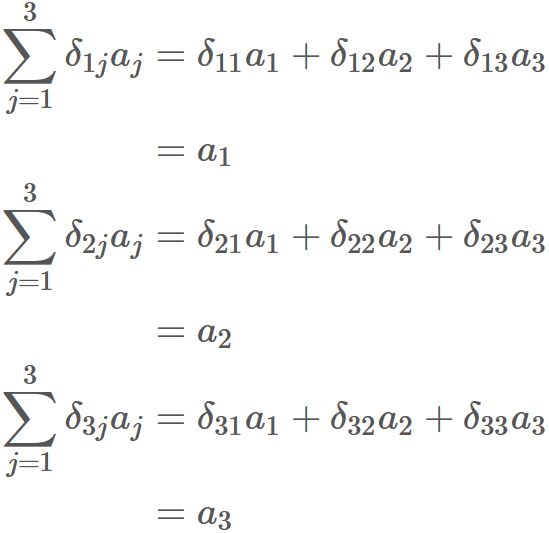
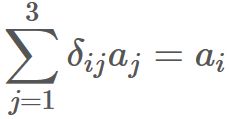
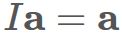
Similarly, let B be an arbitrary 3x3 matrix defined as
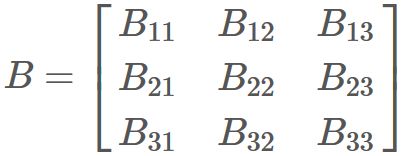
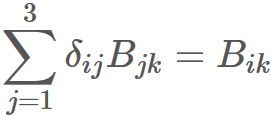
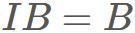
Orthonormal basis
Let $\{ \mathbf{e}_{1}, \mathbf{e}_{2}, \mathbf{e}_{3} \}$ be an orthonormal basis on three dimensional space.
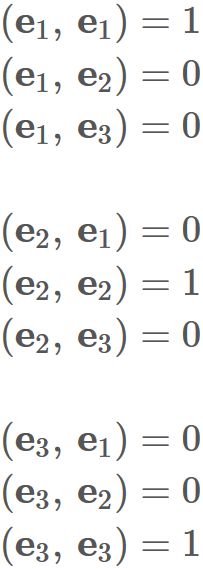
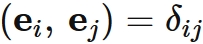
Inner product
Let $A$ and $B$ be arbitrary three-dimensional vectors $A$ and $B$.
These can be expressed as
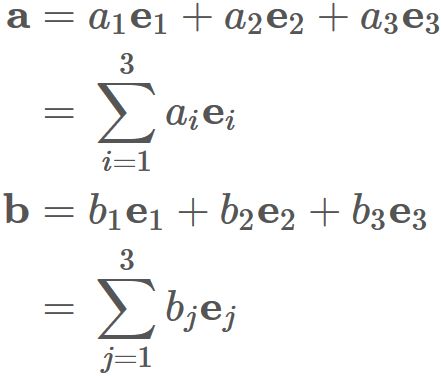
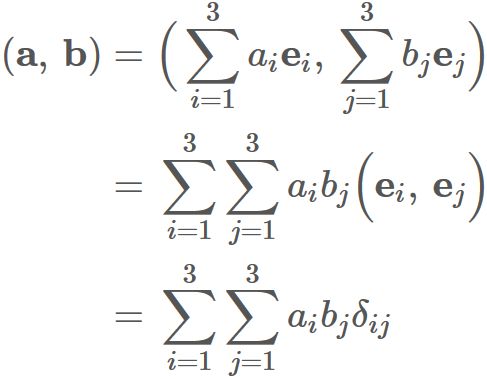
Using $(1)$, we see that the right-hand side is equal to the the standard inner product,
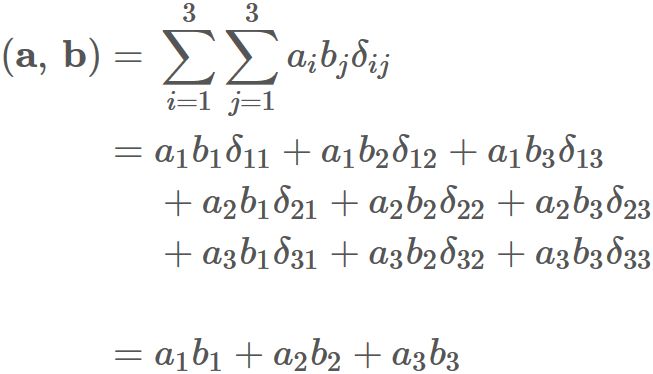
Trace
Let $B$ be an arbitrary 3x3 matrix.
By multiplying each component of $B$ by Kronecker's delta
and summing it over all the components,
it becomes equal to the trace of $B$.
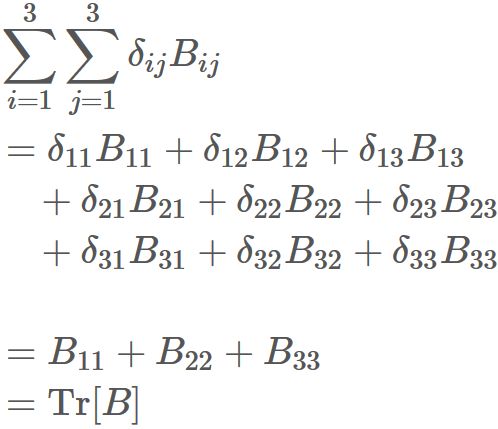
Although the above properties were proved only in the case of three dimensions,
it is also true in the case of arbitrary finite dimensions.