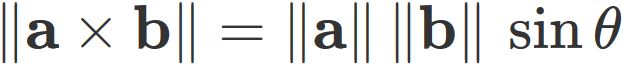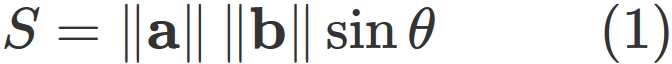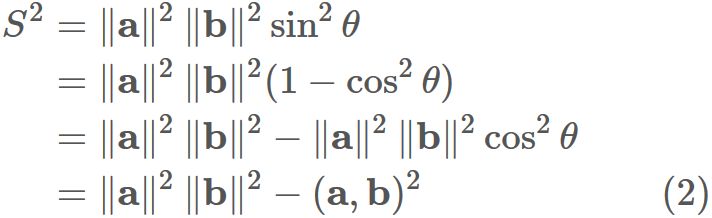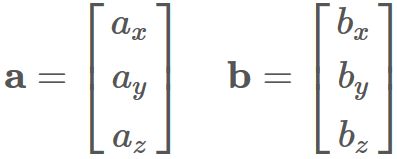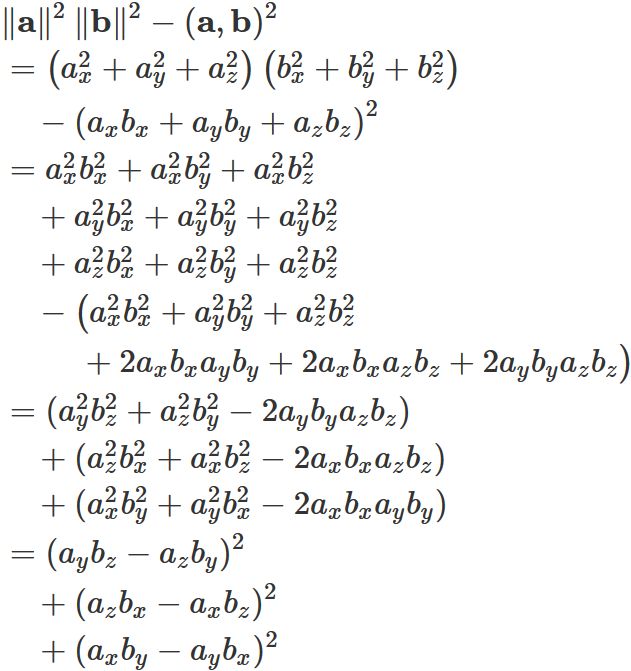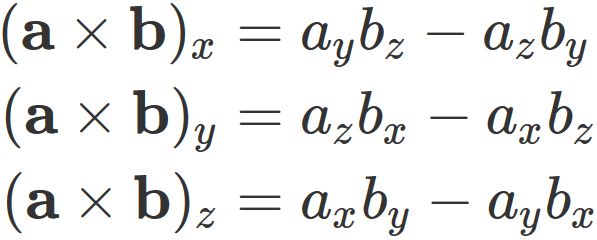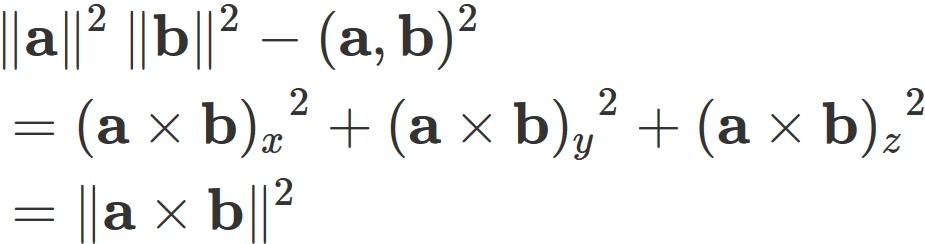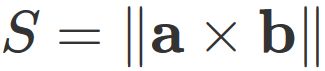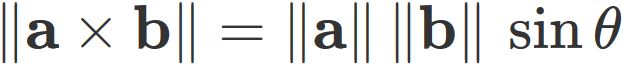Length of Cross Product = Parallelogram Area

  The length (norm) of cross product of two vectors is equal to the area of the parallelogram given by the two vectors, i.e., , where $\theta$ is the angle between vector $ \mathbf{a} $ and vector $ \mathbf{b} $, and $0 \leq \theta \leq \pi$.

  Proof

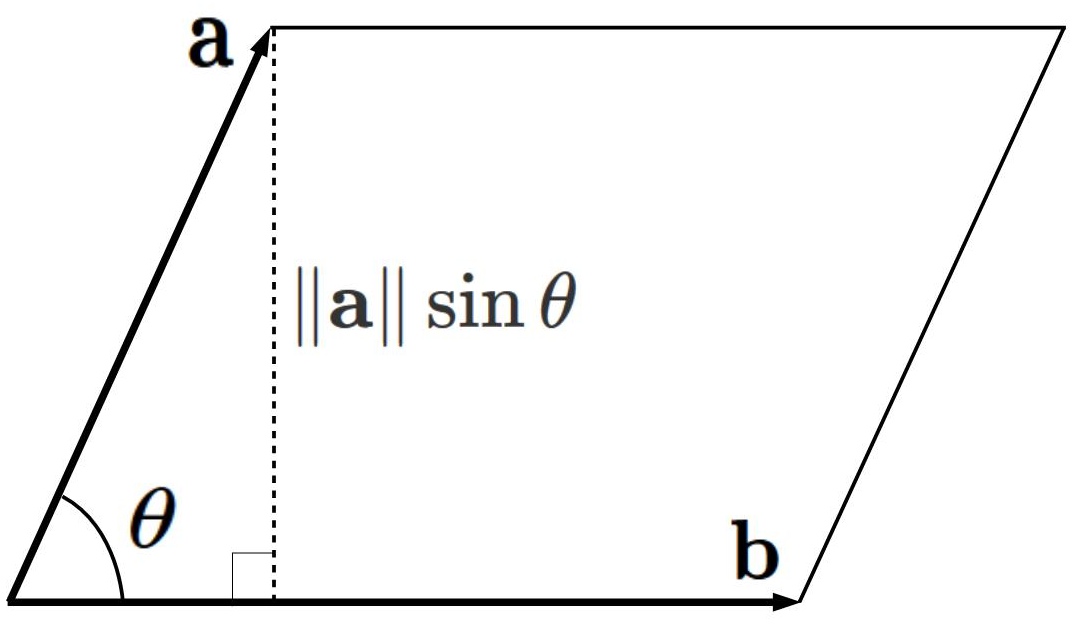
  Let $S$ be the area of a parallelogram formed by two vectors $\mathbf{a}$ and $\mathbf{b}$ (See figure below). The base of this parallelogram is $\| \mathbf{b} \|$ and its height is $\| \mathbf{a} \| \sin\theta$. Therefore,
  By squaring $S$, we have , where we used the relation between inner product and cosine, in the last equality.
  Caluculating the right-hand side of $(2)$ by element, we have The three terms in the last line are the elements of the cross product, $\mathbf{a} \times \mathbf{b}$, i.e., Therefore, we have From this relation and equation $(2)$, we obtain In this way, the area of the parallelogram is equal to the length (norm) of the cross product.
  By substituing $(1)$, this theorem can be written as We thus see that the length of the cross product of two vectors is equal to the product of the length of each vector and the sine of the angle between the two vectors.