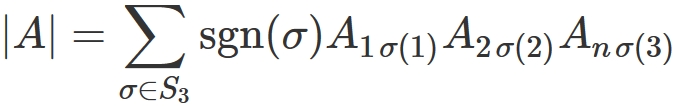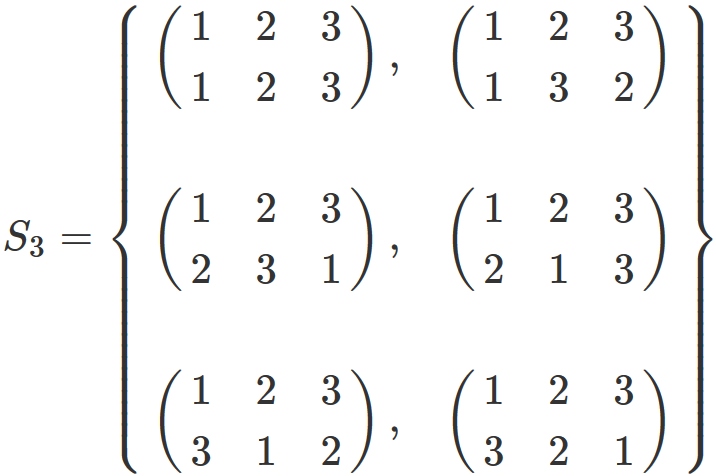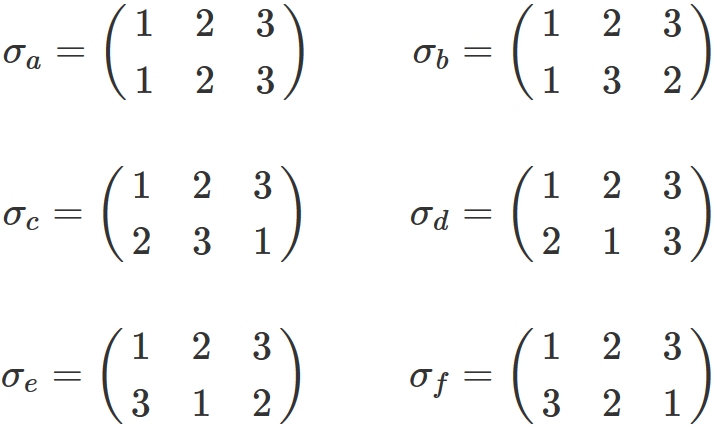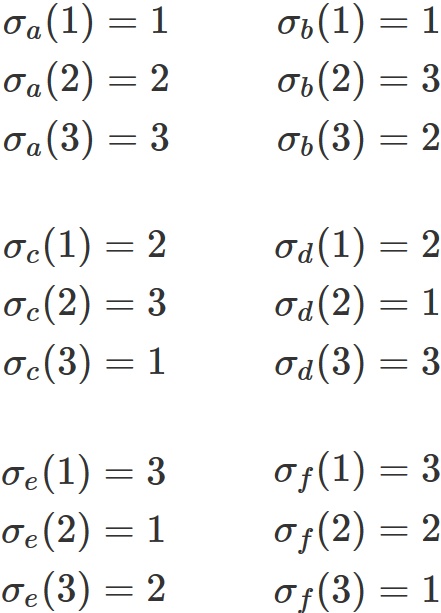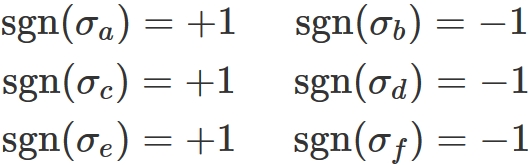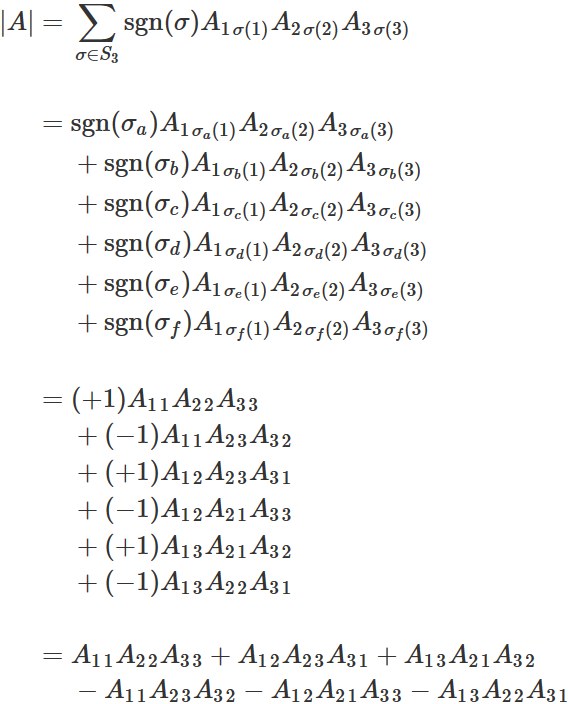Definition of Determinant - SEMATH INFO -
The determinant of a $n \times n $ matrix $A$ is defined as
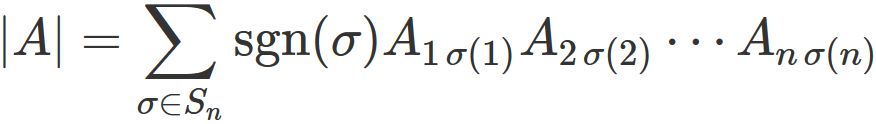
Explanation
We explain the definitions of symbols included in the definition of the determinant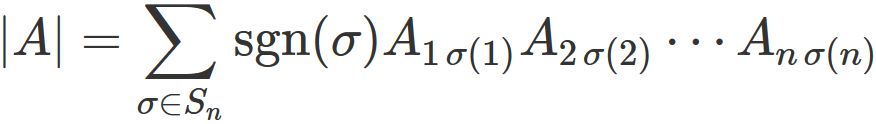
Permutation $\sigma$
The permutation $\sigma$ for a natural number $n$
is a one-to-one mapping that transforms a set $\{1,2,\cdots, n\}$ to the same set.
It is easy to understand by referring to the examples below.
$n=2$
In this case,
the permutation $\sigma$ is a one-to-one mapping
that transforms the set $\{ 1,2 \}$ to the same set.
There are two kinds of mappings.
One is a mapping that transforms $1$ to $1$ and $2$ to $2$,
that is
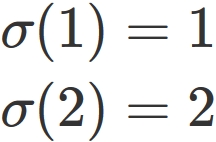
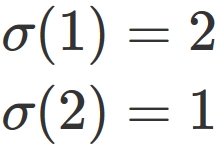
The former is represented by
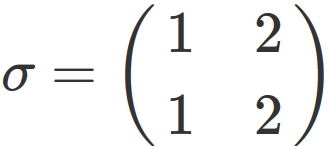
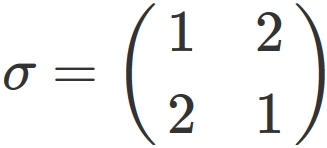
$n=3$
In this case,
the permutation $\sigma$ is a one-to-one mapping
that transforms the set $\{ 1,2,3 \}$ to the same set, and there are six kinds of mappings.
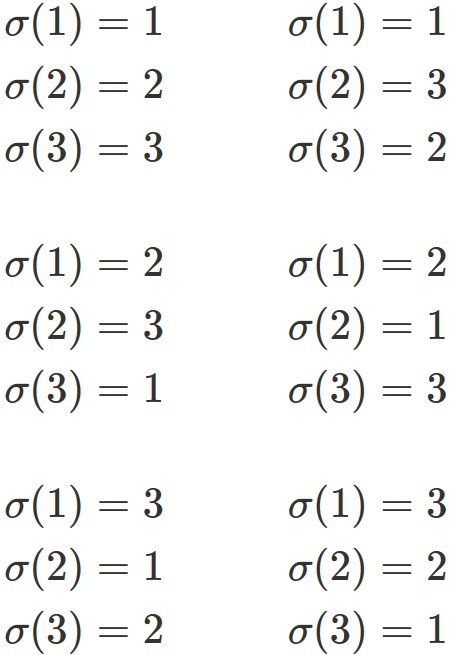
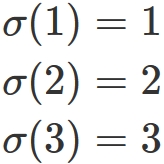
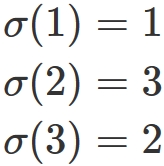
They are sometimes expressed collectively as
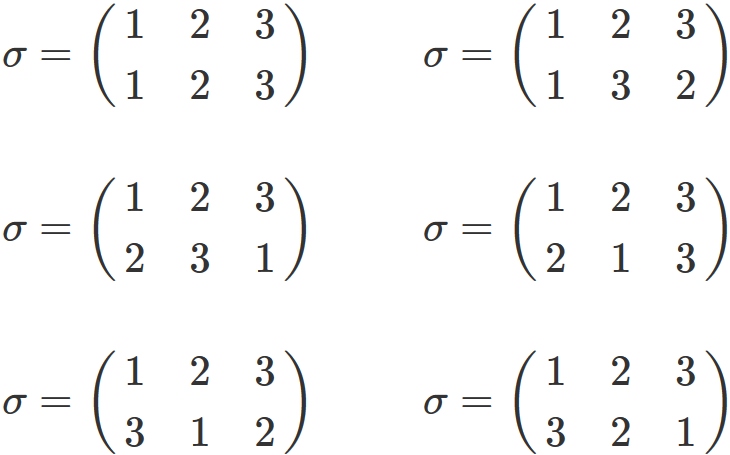
Since the permutation is a one-to-one mapping
that transforms the set $\{1,2, ..., n \}$ to the same set,
it results in a mapping that just rearranges the order of the set.
This can be seen from the examples above.
Set of permutations $S_{n}$
$S_{n}$ is the set of all the permutations, and is also called permutation group.
This is also easy to understand by referring to the following examples.
$n=2$
In this case,
there are two permutations
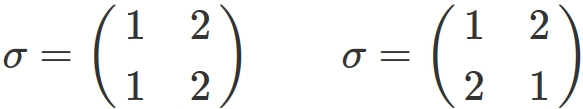
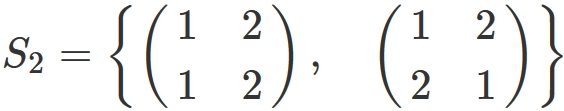
$n=3$
In this case,
there are six permutations
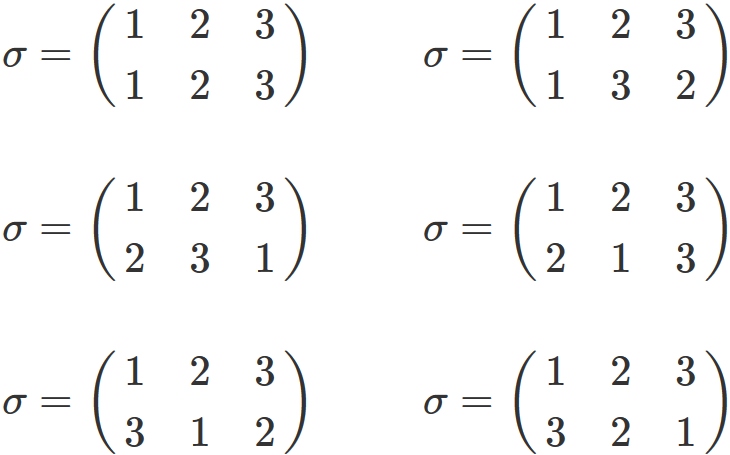
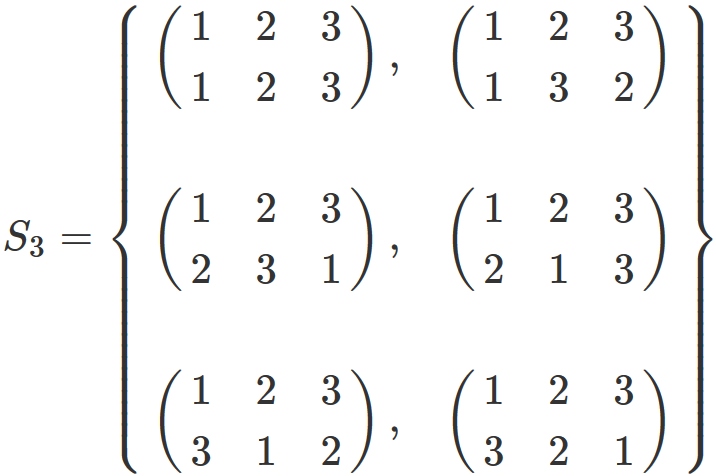
Even permutation and odd permutation
The permuation $\sigma$ is a mapping that only changes the order of the set $\{1,2 \cdots, n\}$. The operation of changing the order is achieved by an operation of exchanging adjacent numbers. For example, the permutation \begin{eqnarray} \left( \begin{array}{c} 1 & 2 & 3 \\ 2 & 3 & 1 \end{array} \right) \end{eqnarray} is a mapping that transforms $\{ 1, 2, 3 \}$ to $\{ 2, 3, 1 \}$, \begin{eqnarray} \begin{array}{c} 1 & 2 & 3 \hspace{1mm} \xrightarrow[ \hspace{5mm}]{\sigma} \hspace{1mm} 2 & 3 & 1 \end{array} \end{eqnarray} . This mapping is achieved by exchanging adjacent numbers two times. First, exchange $1$ and $2$ in $\{ 1, 2, 3 \}$ and make it $\{ 2, 1, 3 \}$, and exchange $1$ and $3$ in $\{ 2, 1, 3 \}$ and make it $\{ 2, 3, 1 \}$ .
If the number of such exchanges is even, the permutation is called even permutation. On the other hand, if the number of such exchanges is odd, the permutation is called odd permutation. It is easy to understand by referring to the following examples.
$n=2$
In this case,
there are two permutations
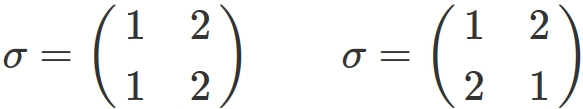
Here, the permutation $\sigma$ on the right side is a mapping that transforms the set $\{1,2\}$ to the set $\{2,1\}$. This can be achived by one exchange, exchanging $1$ and $2$ in the set $\{1,2\}$. Therefore, this permutation is an odd permutation.
On the other hand, the permutation $\sigma$ on the left side is a mapping that transforms the set $\{1,2\}$ to the set $\{1,2\}$. This can be achived by exchanging nothing (zero times exchange). Therefore, this permutation is an even permutation.
From the above it can be seen that in the case of $n = 2$, there are one odd permutation and one even permutation in the set $ S _ {2} $.
$n=3$
In this case,
there are six permutations
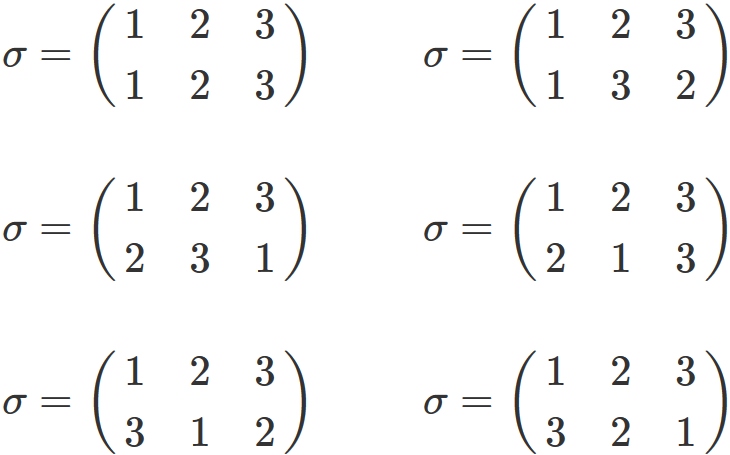
For example,
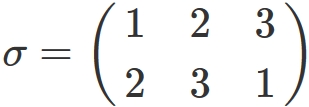
On the other hand,
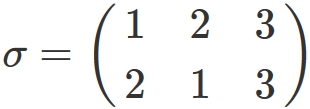
Sign of permutation $\mathrm{sgn}(\sigma)$
The sign of permutation $\mathrm{sgn}$ is a function of permutation $\sigma$
that assigns $+1$ if $\sigma$ is even permutation and $-1$ if it is odd permutation.
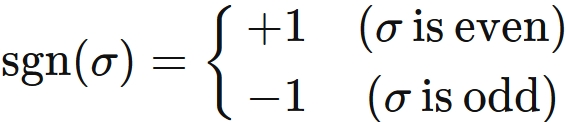
$n=2$
In this case,
there are two permutations mentioned above.
In them,
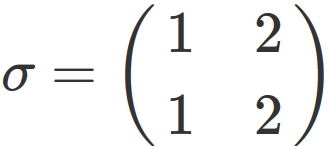
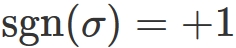
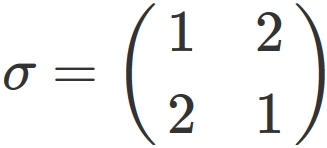
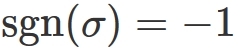
$n=3$
In this case, there are six permutations as mentioned above.
In them,
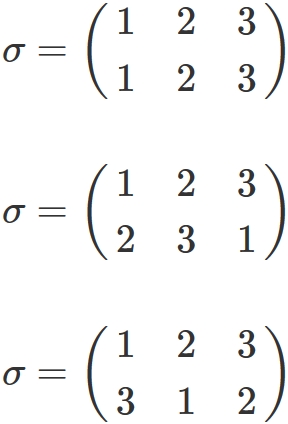
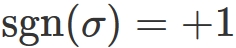
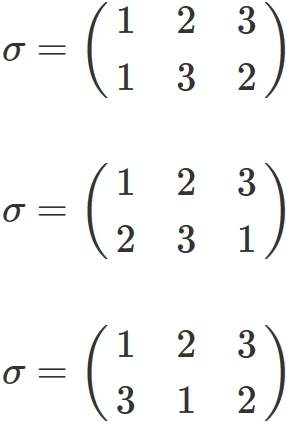
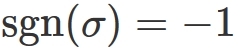
Definition of determinant
The definition of the determinant of an $n$ x $n$ matrix $A$ is
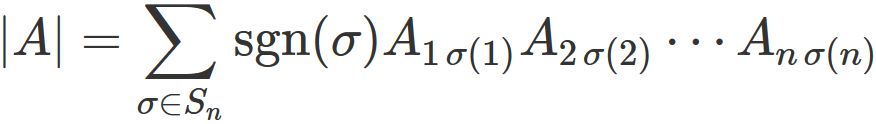
First, $\sigma (i)$ appearing in the suffix of $A$ is a value obtained by transforming the natural number $i$ by the permutation $\sigma$. For example, if $n=3$ and the permutation is
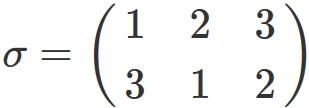
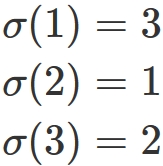
$\mathrm{sgn}(\sigma)$ is the sign of the permutation $\sigma$ and it takes a value of $+1$ for any even permutation and $-1$ for any odd permutation. For example, in the case of
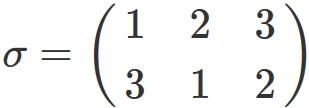
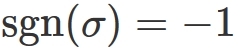
Finally, the summation
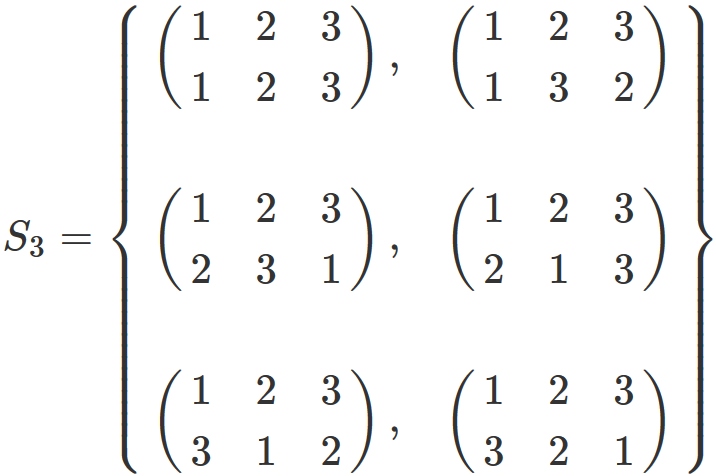
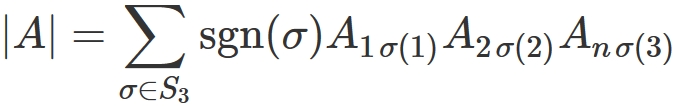
Example ($n=2$)
In this case,
the definition of the determinant is
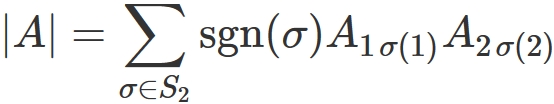
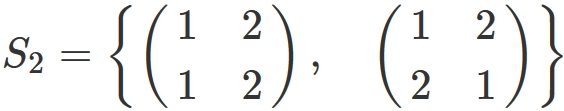
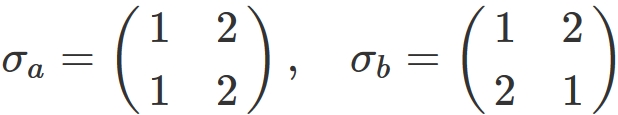
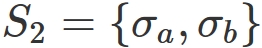
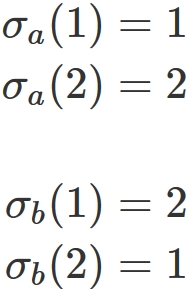
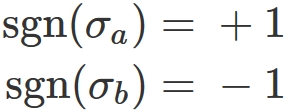
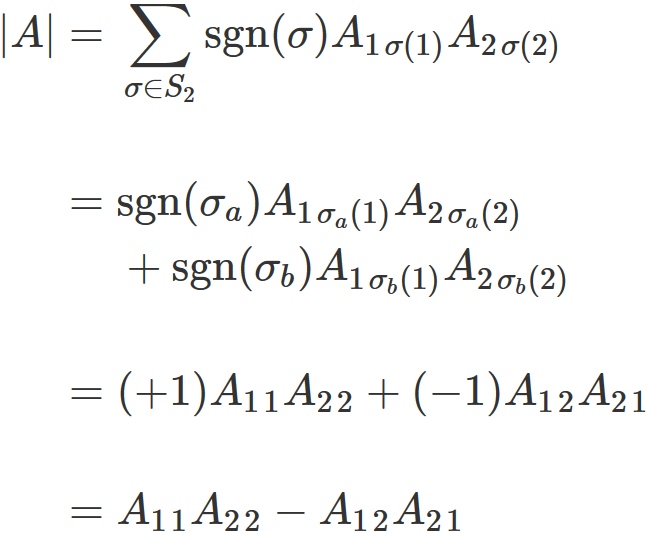
Example ($n=3$)
In this case,
the definition of the determinant is