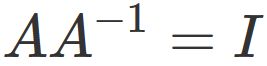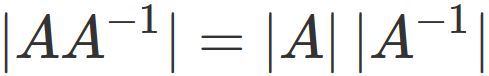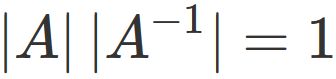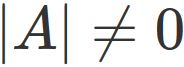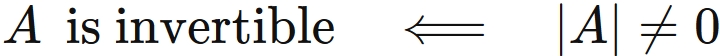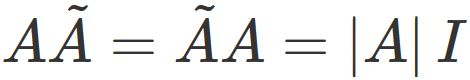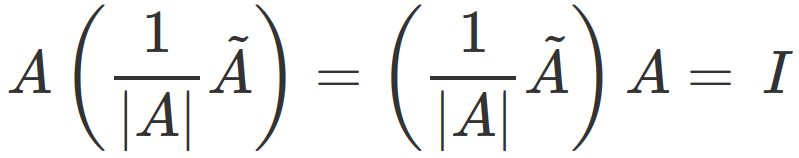"Invertible Matrix" ⇔ "Non-zero determinant" - SEMATH INFO -

  A matrix is invertible if and only if its determinant is non-zero, i.e., .

Proof

  First we will prove .
  If $A$ is an invertible matirx. there exists an inverse matrix $A^{-1}$ satisfying . The determinant of the left-hand side of this equation can be represented as the product of the determinants, i.e., , because, in general, the determinant of the product is equal to the product of the determinants. On the other hand, the determinant of the right-hand side of the equation (the identity matrix) is $1$. We thus see that . Therefore $|A|$ must not be zero, that is,   Next we will prove .
  It is known that the product of a square matrix and its adjugate matrix is equal to the product of the identity matrix and the determinant, i.e., where $\tilde{A}$ is the adjugate matrix of $A$.
  If $|A|\neq 0$, we see that . This equation means that the matrix $ \frac{1}{| A |} \tilde{A} $ is the inverse of $ A $. Therefore, the inverse matrix of $A$ exists, that is, $A$ is invertible.   The following statement is obtained from the above. .