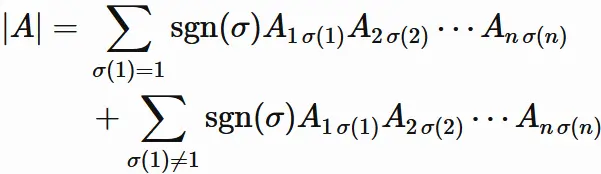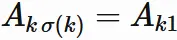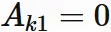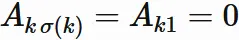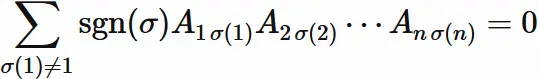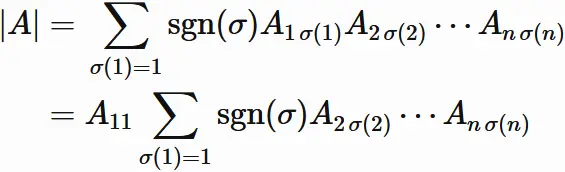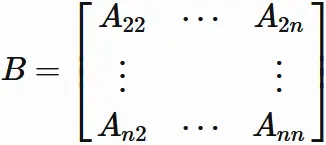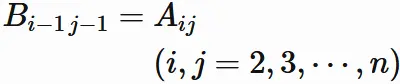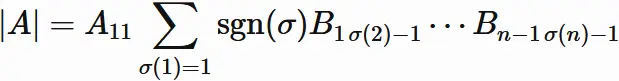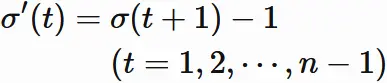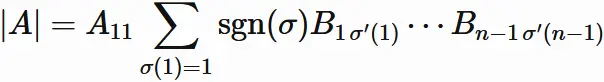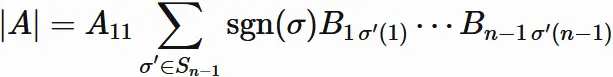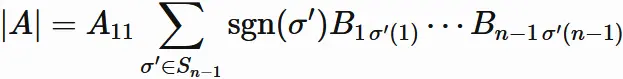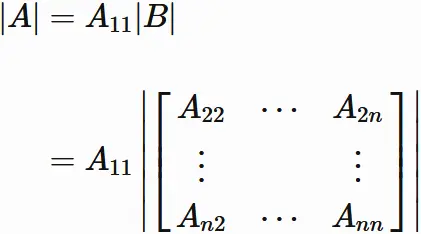Determinant properties and formulas
Swap rows and columns
Let $A^{(i\leftrightarrow j)}$ be a matrix given by
swapping the $i$-th and $j$-th columns of a matrix $A$.
Its determinant differs from the original determinant only in sign:
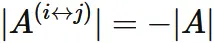
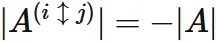
Proof
● $| A^{(i\hspace{1mm} \updownarrow \hspace{1mm}j)} | = -|A|$
Let $A_{kl}$ be the $k$-th row and $l$-th column element of an $n \times n$ matrix of $A$. The determinant of $A$ is
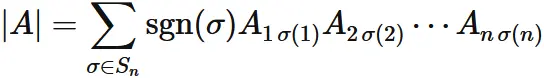(See "Definition of determinant").
Here, the sign of the permutation is
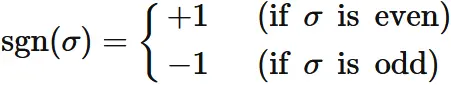$$
\tag{1.3}
$$
Focusing on the $i$ and $j$ rows,
let us write $|A|$ as
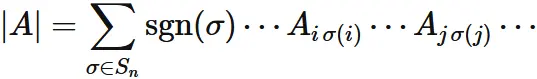Let $A^{(i\hspace{1mm} \updownarrow \hspace{1mm}j)}$ be a matrix given by swapping the $i$ and $j$ rows of $A$,
and $A^{(i \hspace{1mm}\updownarrow \hspace{1mm}j)}_{kl}$
be the $k$-th row and $l$-th column element of $A^{(i\hspace{1mm} \updownarrow \hspace{1mm}j)}$.
We have
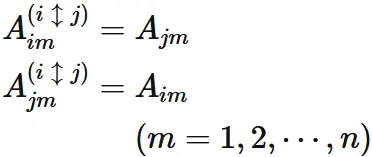The determinant of
$A^{(i \hspace{1mm}\updownarrow \hspace{1mm}j)}$ is
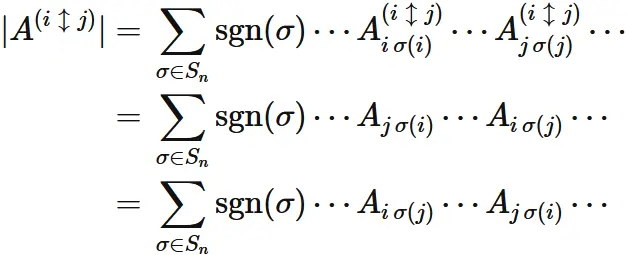$$
\tag{1.4}
$$
Here,
the last line only changes the order of multiplication.
Let $\xi$ be a permutation that swaps $\sigma(i)$ and $\sigma(j)$:
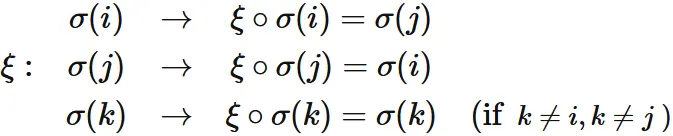$$
\tag{1.5}
$$
For example,
if $\sigma$ is
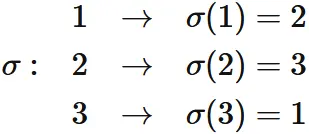and if $\xi$ swaps $\sigma(1)$ and $\sigma(3)$,
then
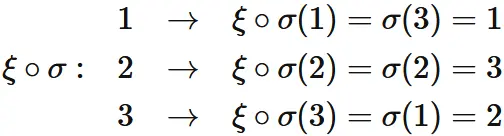Using $(1.5)$,
$(1.4)$ can be expressed as
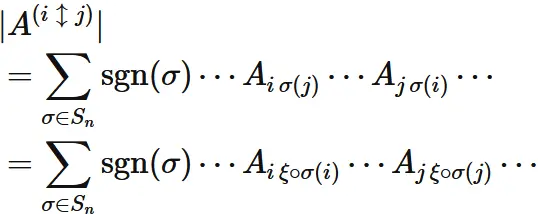$$
\tag{1.6}
$$
The permutation $\xi$ is an odd permutation
because it swaps only once.
Therefore,
if $\sigma$ is an even permutation,
the composite permutation $\xi \circ \sigma(\cdot)$
is an odd permutation,
and if $\sigma$ is an odd permutation,
the composite permutation $\xi \circ \sigma(\cdot)$
is an even permutation.
We therefore see that
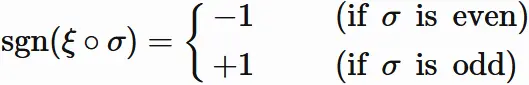$(1.3)$ and this give
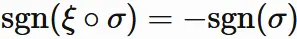holds for any permutation $\sigma$.
Using this, $(1.6)$ can be written as
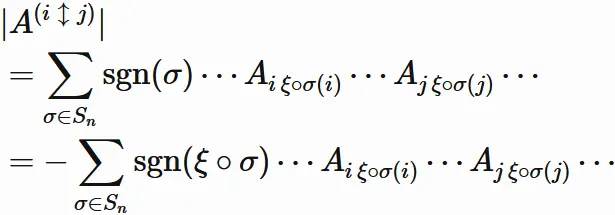$$
\tag{1.7}
$$
The permutation $\sigma$ is a mapping that only changes the order of the set
$
\{1,2,\cdots,n\}.
$
For example, if $n=3$,
all the permutations $\sigma$ are
If $\xi$ swaps $\sigma(1)$ and $\sigma(3)$,
all the composite permutations $\xi \circ \sigma $ are
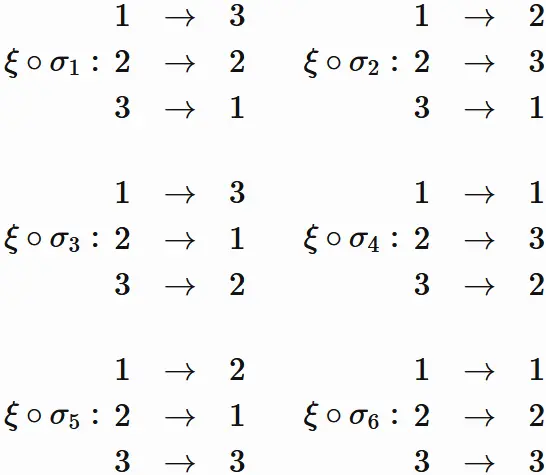As seen this example,
the composite permutation $\xi \circ \sigma$ is also a mapping that only changes the order.
And
the set
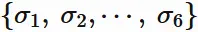is identical to the set
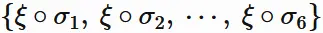Therefore,
the summation
$\sum_{\sigma \in S_{n}}$ in $(1.7)$
can be replaced with
$\sum_{\xi \circ \sigma \in S_{n}}$:
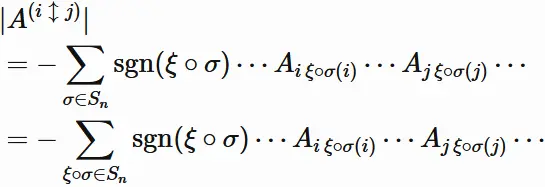Let $\tau$
be
$\xi \circ \sigma$. We have
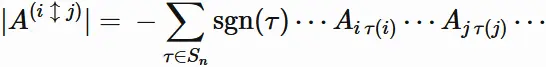The right hand side is equal to -$|A|$.
So we obtain
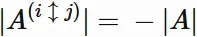
● $| A^{(i \leftrightarrow j)} | = -|A|$
First, applying the same discussion as above to the transposed matrix $A^{T}$ , we have
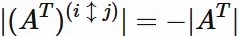Generally,
a matrix transposed after swapping columns
is equal to a matrix swapping rows after transpose:
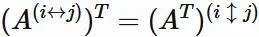We obtain
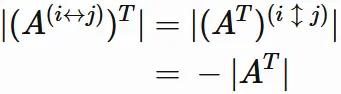Finally,
the matrix transpose property ( $|A^{T}| = |A|$)
gives
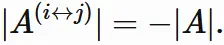
● $| A^{(i\hspace{1mm} \updownarrow \hspace{1mm}j)} | = -|A|$
Let $A_{kl}$ be the $k$-th row and $l$-th column element of an $n \times n$ matrix of $A$. The determinant of $A$ is
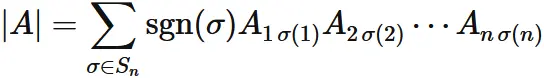
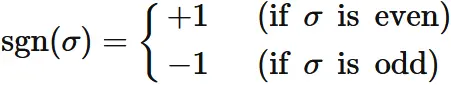
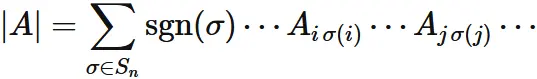
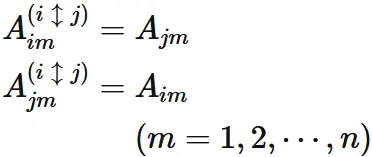
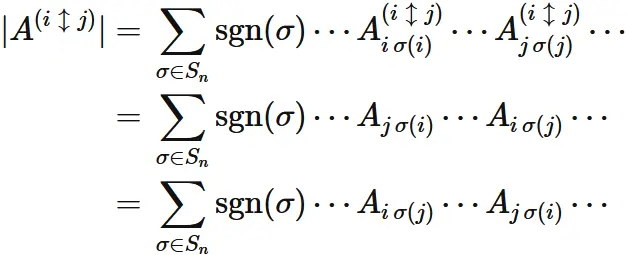
Let $\xi$ be a permutation that swaps $\sigma(i)$ and $\sigma(j)$:
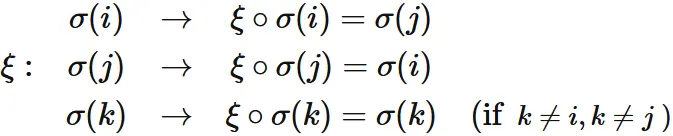
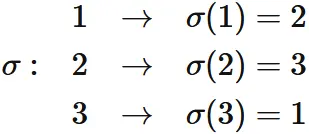
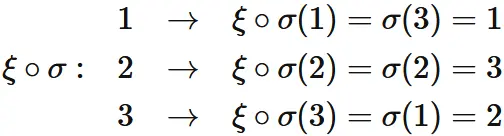
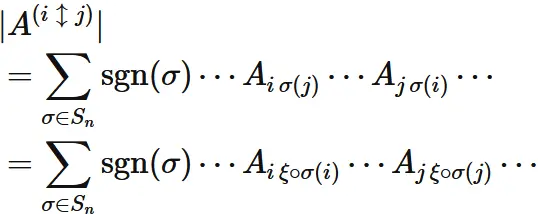
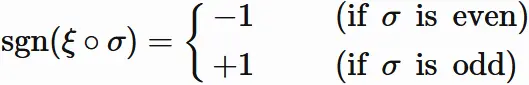
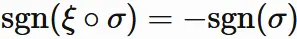
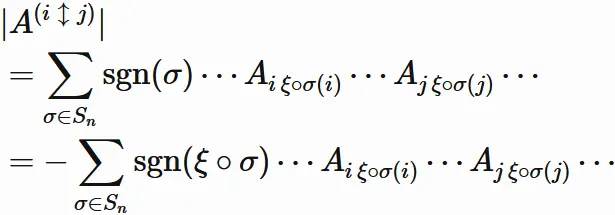
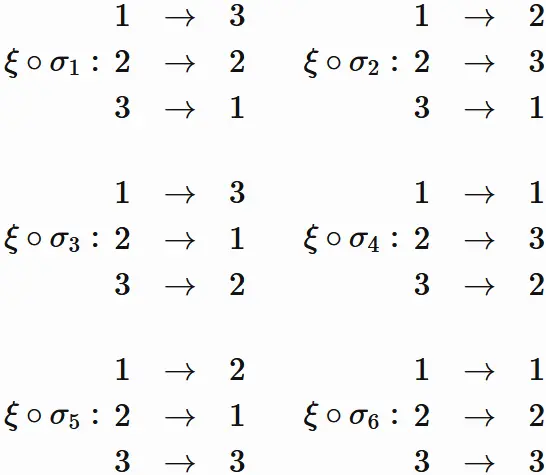
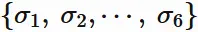
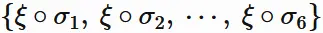
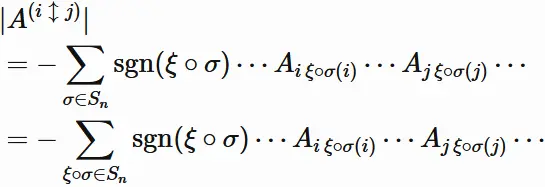
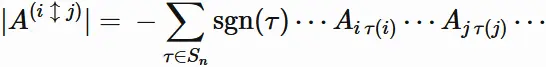
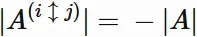
● $| A^{(i \leftrightarrow j)} | = -|A|$
First, applying the same discussion as above to the transposed matrix $A^{T}$ , we have
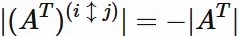
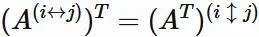
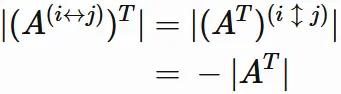
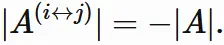
Case two columns are equal
Let
$\mathbf{a}_{i}$
and
$\mathbf{a}_{j}$
$(i \neq j)$
denote the $i$-th and $j$-th column vectors of an $n \times n$ matrix $A$,
respectively,
and denote $A$ as
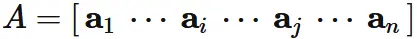
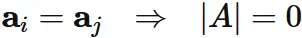
Proof
Let $A^{(i\leftrightarrow j)}$ be a matrix given by swapping the $i$-th and $j$-th columns of $A$.
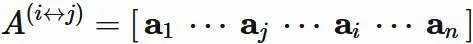By $(1.1)$, we have
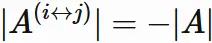$$
\tag{2.2}
$$
If
$
\mathbf{a}_{i} = \mathbf{a}_{j}
$
,
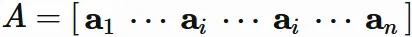In this case,
swapping the $i$-th and $j$-th column vectors does not change the matrix..
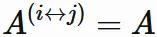Eq. $(2.2)$ and this give
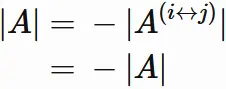We obtain
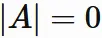
Let $A^{(i\leftrightarrow j)}$ be a matrix given by swapping the $i$-th and $j$-th columns of $A$.
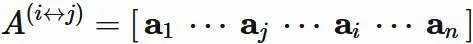
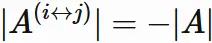
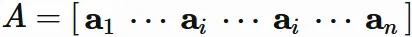
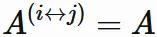
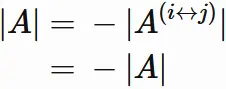
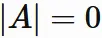
Case two rows are equal
Let
$\mathbf{a}_{i}$
and
$\mathbf{a}_{j}$
$(i \neq j)$
denote the $i$-th and $j$-th row vectors of an $n \times n$ matrix $A$,
respectively,
and denote $A$ as
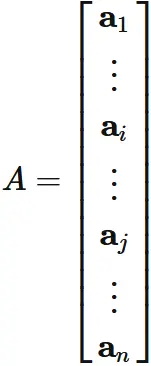
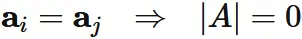
Proof
Let $A^{(i\hspace{1mm}\updownarrow\hspace{1mm} j)}$ be a matrix given by swapping the $i$-th and $j$-th rows of $A$.
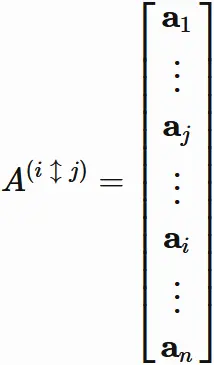Its determinant differs from the original determinant
only in sign
(see the above).
$$
\tag{3.2}
$$
If
$\mathbf{a}_{i} = \mathbf{a}_{j}$,
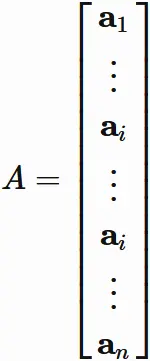In this case,
swapping the $i$-th and $j$-th rows does not change the matrix.
Therefore
Eq. $(3.2)$ and this give
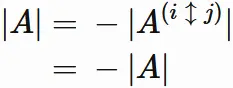We obtain
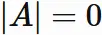
Let $A^{(i\hspace{1mm}\updownarrow\hspace{1mm} j)}$ be a matrix given by swapping the $i$-th and $j$-th rows of $A$.
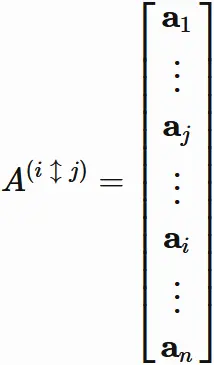
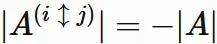
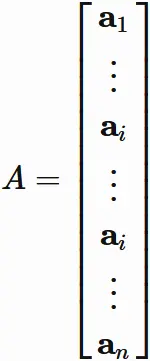
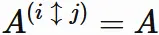
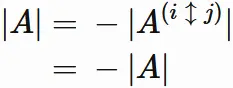
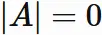
Case if a row is scalar-multiplied
Let $A_{ij}$
be the $i$-th row
and $j$-th column element of an $n \times n$ matrix $A$:
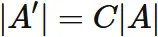
Proof
Let $A'_{ij}$ be the $i$-th row and $j$-th column element of $A$. The determinant of $A'$ is
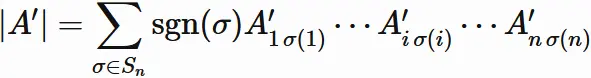(See definition of determinant).
By $(4.1)$ and $(4.2)$,
we have
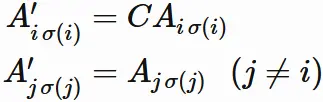Therefore we obtain
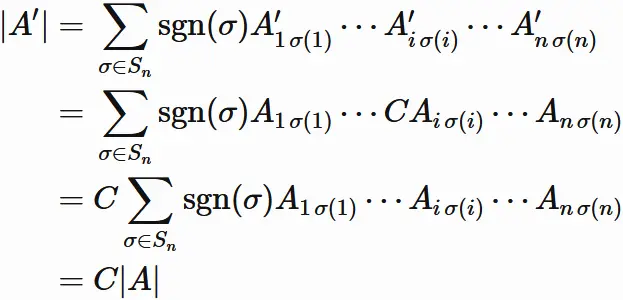
Let $A'_{ij}$ be the $i$-th row and $j$-th column element of $A$. The determinant of $A'$ is
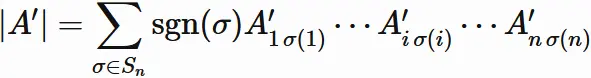
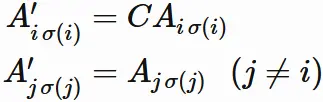
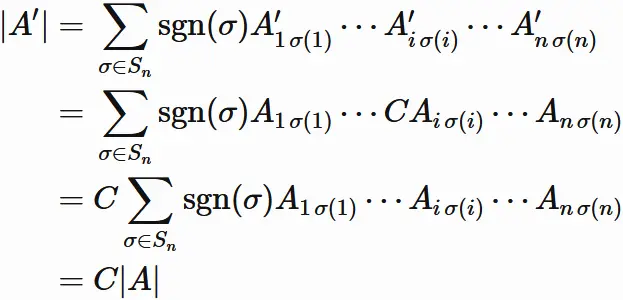
Case if a column is scalar-multiplied
Let $A_{ij}$
be the $i$-th row
and $j$-th column element of an $n \times n$ matrix $A$:
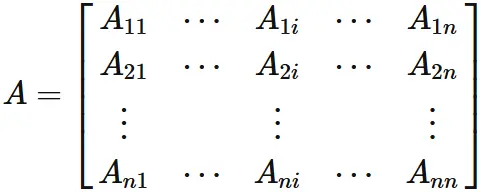
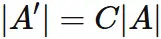
Proof
Since the determinant of transpose of $A$ is equal to the determinant of $A$ , we have
By
(4.3),
we obtain
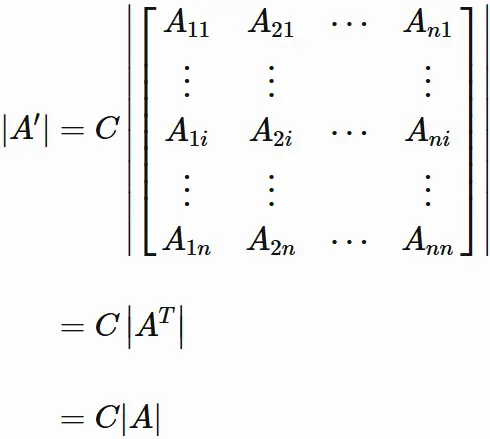
Since the determinant of transpose of $A$ is equal to the determinant of $A$ , we have
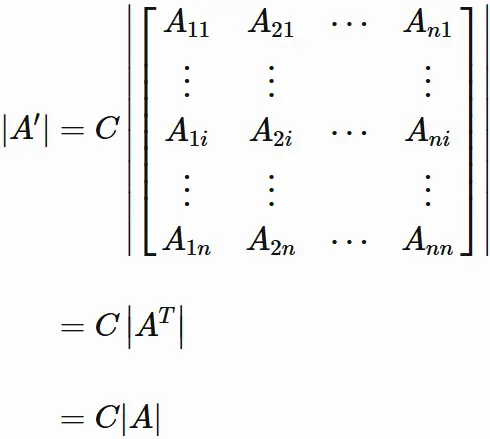
Case if a scalar is multiplied
Let $A$ be an $n \times n$ matrix.
The determinant of $A$ multiplied by a scaler $\alpha$
is $\alpha^n$ times the determinant of $A$.
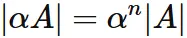
Proof
By definition of determinant, the determinant of $A$ is
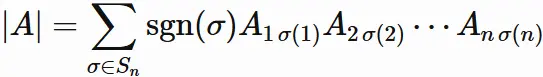where $A_{ij}$ is the $i$-th row and $j$-th column element of $A$,
$\sigma$ is the permutation,
$S_{n}$ is
the set of all the permutations,
and
$\mathrm{sgn}(\sigma)$ is the sign of permutation.
In the same way, the determinant of $\alpha A$ is
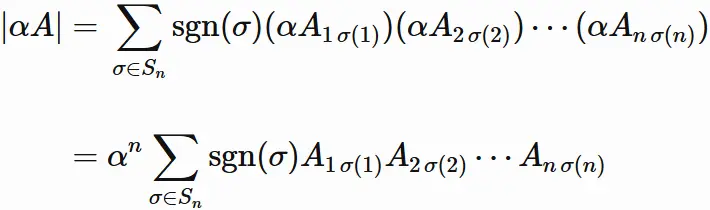Therefore, we obtain
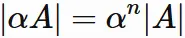
By definition of determinant, the determinant of $A$ is
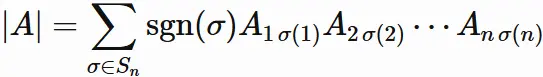
In the same way, the determinant of $\alpha A$ is
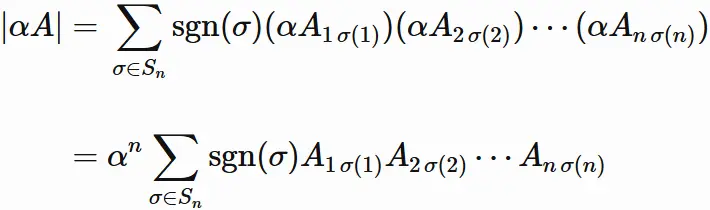
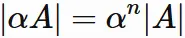
Case if a row vector is sum
Let $A$ be an $n \times n$ matrix,
and $\mathbf{a}_{i}$ be the $i$-th row vector of $A$.
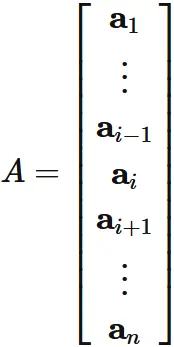
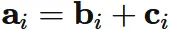
Proof
From $(7.1)$ and $(7.2)$, the determinants of $|A|$, $|B|$, and $|C|$ are
Let
$A_{ij}$,
$B_{ij}$,
and
$C_{ij}$
be the $i$-th row and $j$-th column element of $A$, $B$, and $C$, respectively.
By definition,
the determinants are
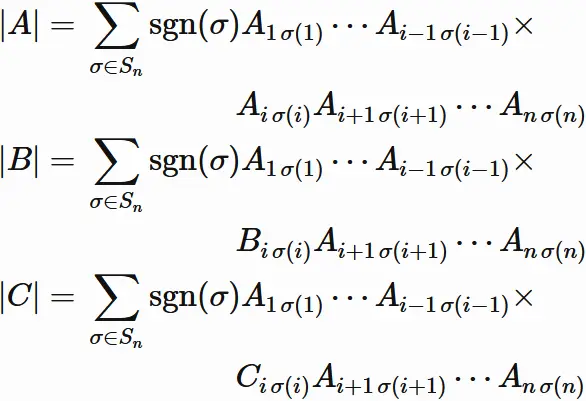From $(7.3)$, we have
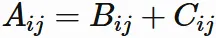We see that
the determinant of $|A|$ can be written as
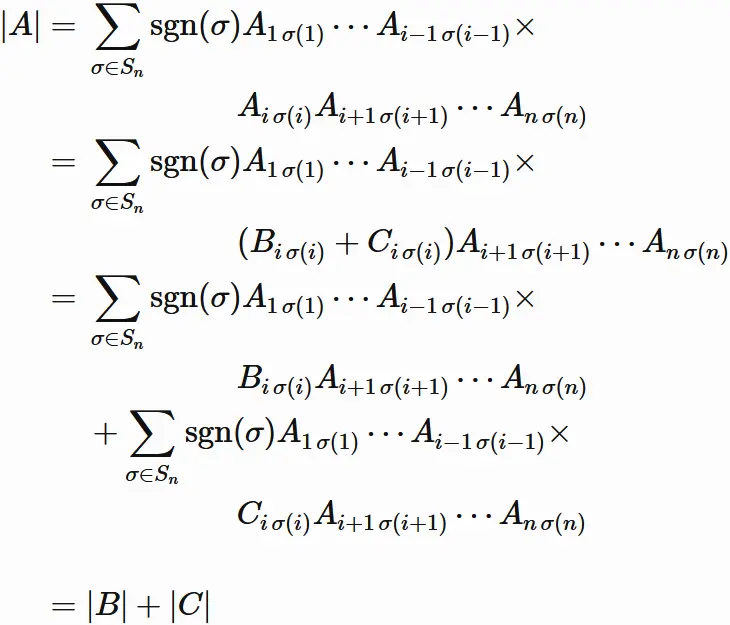We have
From $(7.1)$ and $(7.2)$, the determinants of $|A|$, $|B|$, and $|C|$ are
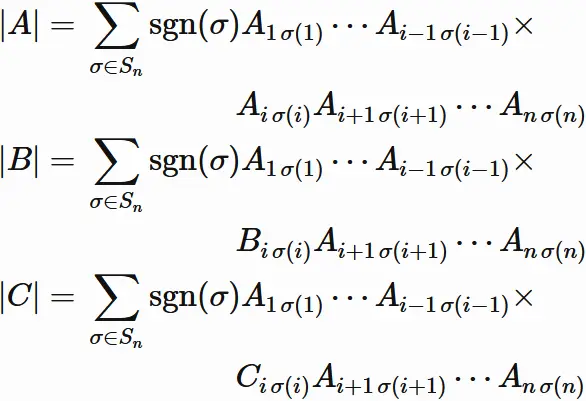
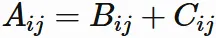
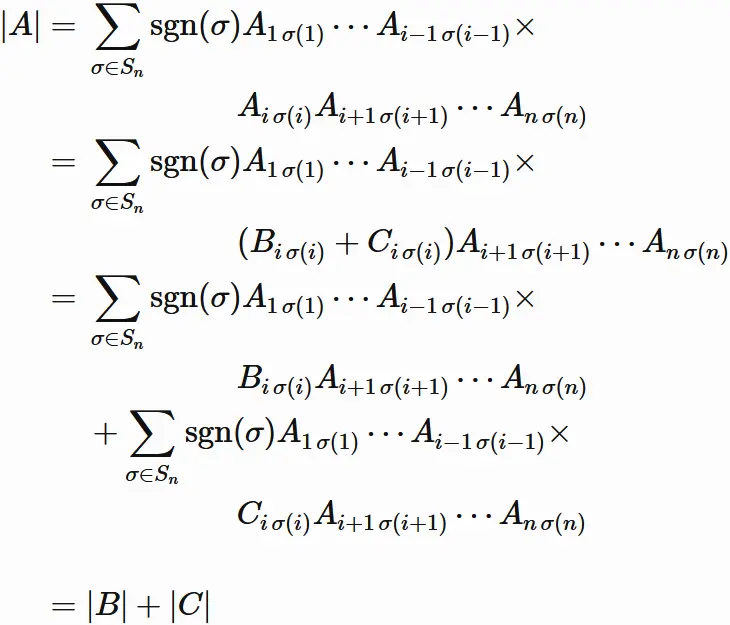
Case if a column vector is sum
Let $A$ be an $n \times n$ matrix,
and $\mathbf{a}_{i}$ be the $i$-th column vector of $A$.
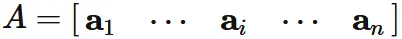
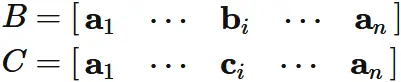
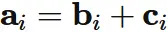
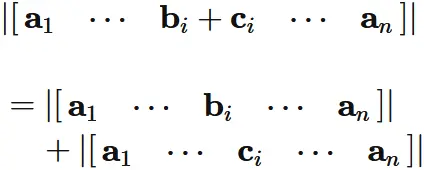
Proof
By $(8.3)$, we have
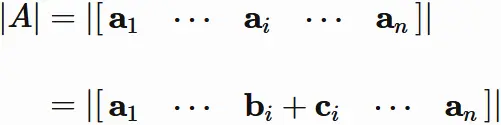Since the determinant of the transposed matrix
is equal to the determinant of the original matrix,
we have
Here,
$\mathbf{b}_{i}^{T} + \mathbf{c}_{i}^{T}$
is the $i$-th row vector of $A^{T}$.
By $(7.4)$,
we have
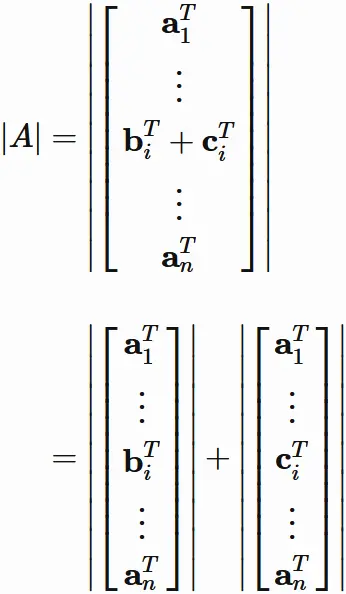For the determinant of each term on the right side,
we use again the property that
the determinant of the transposed matrix
is equal to the determinant of the original matrix, and obtain
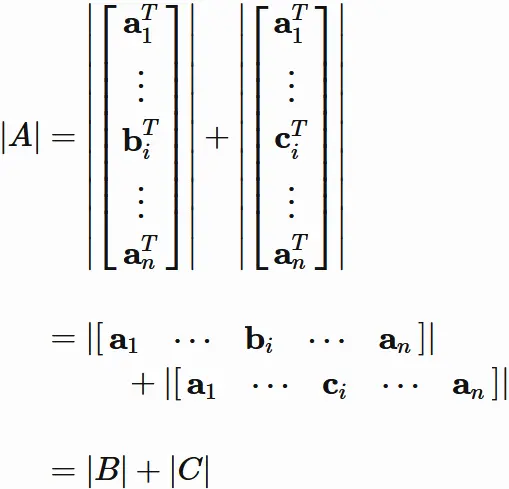
By $(8.3)$, we have
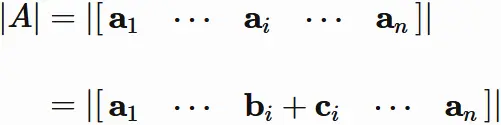
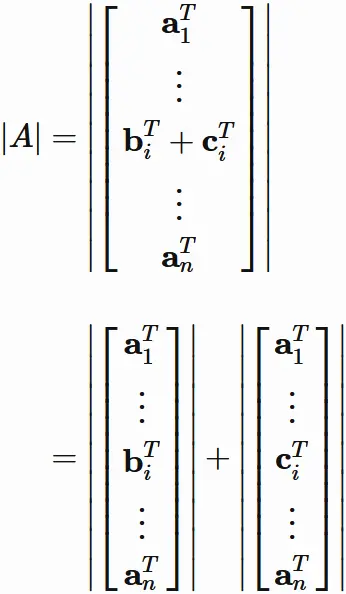
Add one row to another
Let $A$ be an $n \times n$ matrix,
and $\mathbf{a}_{i}$ be the $i$-th row vector of $A$.
Let $A'$ be an $n \times n$ matrix given by adding the scalar multiple of $j$-th row vector of $A$ to $A$:
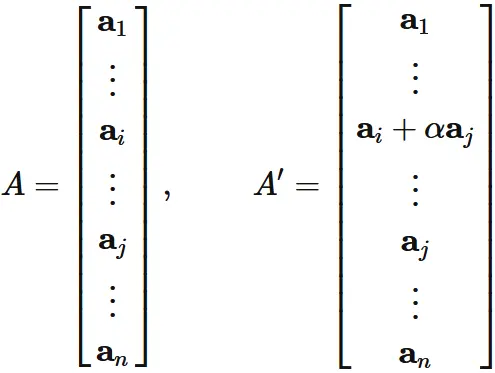
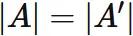
Proof
By (7.4), we have
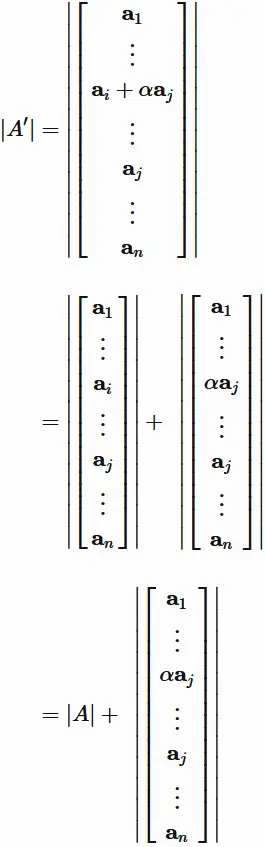Applying $(4.3)$ and $(3.1)$ to the second term of the righthand side,
we have
Therefore we obtain
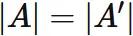
By (7.4), we have
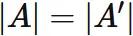
Case if the 1st column is 1000...
Let $A$ be
an $n \times n$
matrix whose elements after the second element in the first column are all $0$:
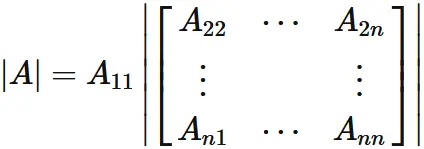
Proof
The determinant of $A$ is
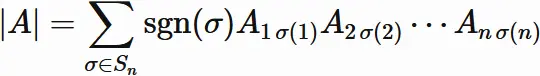$$
\tag{10.3}
$$
where $ A_{ij}$ $(i,j=1,2,\cdots,n)$ is
the $i$-th row and $j$-th column element of $A$,
$\sigma$ is the permutation,
$S_{n}$ is
the set of all the permutations,
and
$\mathrm{sgn}(\sigma)$ is the sign of permutation (See "Determinant definition").
Let us write $(10.3)$ by dividing it into the summation for $\sigma(1) = 1$ and the summation for $\sigma(1)\neq 1$.
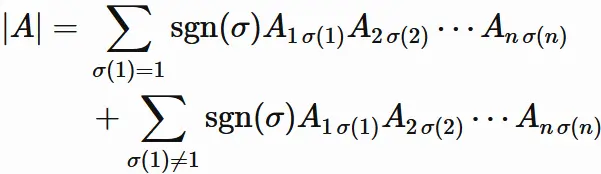$$
\tag{10.4}
$$
Since the permutation $\sigma$ is a one-to-one mapping from $\{1,2,⋯,n \}$ to $\{1,2,⋯,n \}$,
if $\sigma(1) \neq 1$,
any one of the integers from $2$ to $n$
satisfies
$\sigma(k) = 1$.
For such $k$ ,
we have
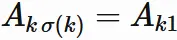$$
\tag{10.5}
$$
By $(10.1)$,
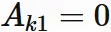We have
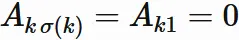and
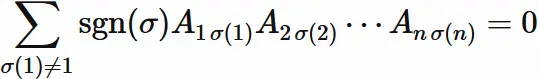This and $(10.4)$ give
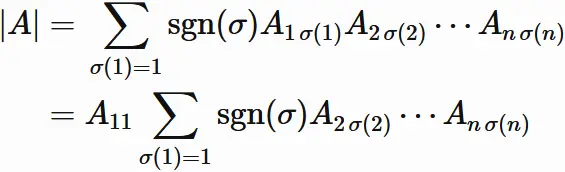$$
\tag{10.6}
$$
Let $B$ an $(n-1)\times(n-1)$ matrix defined as
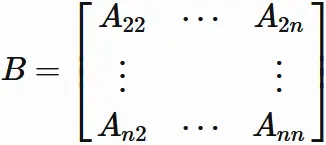and $B_{ij}$ be
the $i$-th row and $j$-th column element of $B$.
We have
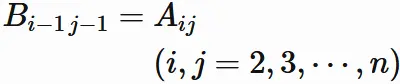Using this,
$(10.6)$ can be written as
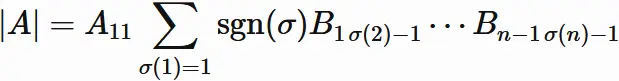Let
$\sigma'$ be a map defined as
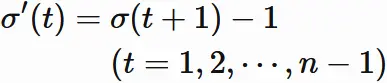$$
\tag{10.7}
$$
We have
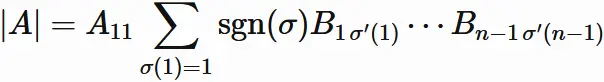Under the condition
$\sigma(1)=1$,
$\sigma$ is a one-to-one map from $\{2,3,\cdots,n \}$ to $\{2,3,\cdots,n \}$.
By $(10.7)$,
$\sigma'$ is a one-to-one map from
$\{1,2,\cdots,n-1 \}$
to
$\{1,2,\cdots,n-1 \}$.
So, $\sigma'$ is a permutation of $\{1,2,\cdots,n-1 \}$ (see "Determinant definition").
We see that
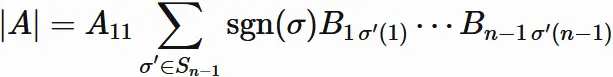where $S_{n-1}$ is the set of all the permutations.
By $(10.7)$,
$\sigma'$ is an even permutation,
if $\sigma$ is an even permutation.
And
$\sigma'$ is an odd permutation,
if $\sigma$ is an odd permutation.
Hence the permutation sign of $\sigma'$ is equal to the permutation sign of $\sigma$:
$
\mathrm{sgn}(\sigma) = \mathrm{sgn}(\sigma').
$
We have
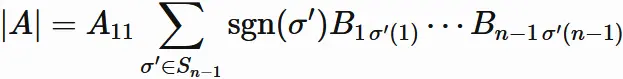The summation of the right-hand side is the determinant of $B$.
We obtain
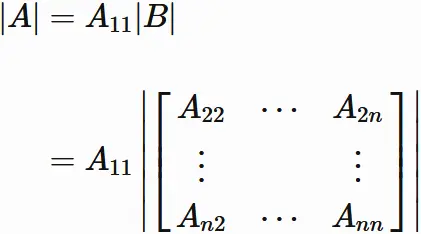
The determinant of $A$ is
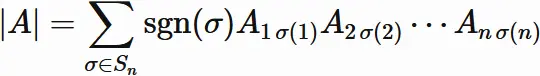
Let us write $(10.3)$ by dividing it into the summation for $\sigma(1) = 1$ and the summation for $\sigma(1)\neq 1$.