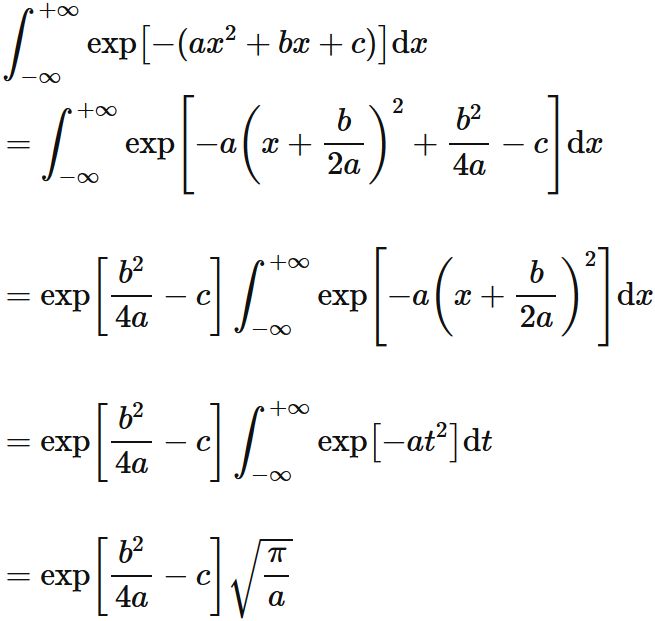Proof of Gaussian Intergral
Gaussian integral
The definition of the Gaussian integral is
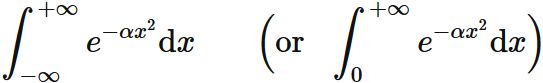
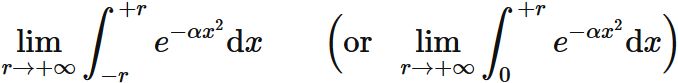
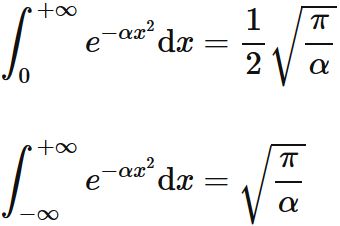
Proof
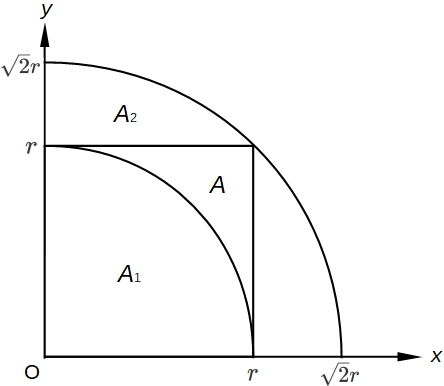
We start with defining three areas in the two dimensional space.
The first area is a closed area $A_{1}$ whose boundary is the x-axis, the y-axis and a circle with radius $r$ centered at the origin.
The second area is a closed area $A$ whose boundary is the x-axis, the y-axis, the line $x=r$, and the line $y=r$. $A$ is a square with an edge length $r$.
The third area is a closed area $A_{2}$ whose boundary is the x-axis, the y-axis and a circle with radius $\sqrt{2}r$ centered at the origin.
In this way, $A_{1}$ is included in $A$ and $A$ is included in $A _ {2}$ (See figure below).
 Let $I_{1}$, $I$, and $I_{2}$ be an integral of $e^{-\alpha (x^{2}+ y^{2})}$ over $A_{1}$, $A$, and $A_{2}$, respectively, i.e.,
Let $I_{1}$, $I$, and $I_{2}$ be an integral of $e^{-\alpha (x^{2}+ y^{2})}$ over $A_{1}$, $A$, and $A_{2}$, respectively, i.e.,
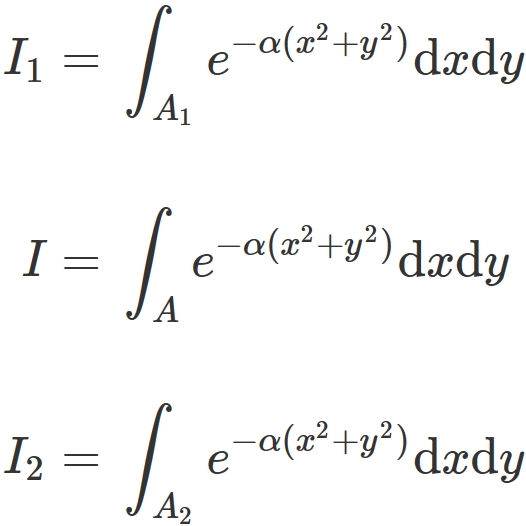 Their integrand is positive, and $A_{1}$ is included in $A$, and $A$ is included in $A _ {2}$.
Therefore the inequality
Their integrand is positive, and $A_{1}$ is included in $A$, and $A$ is included in $A _ {2}$.
Therefore the inequality
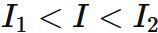 $$
\tag{1}
$$
holds.
By using polar coordinates,
$$
\tag{1}
$$
holds.
By using polar coordinates,
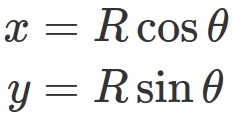 ,
the integral $I_{1}$ can be written as
,
the integral $I_{1}$ can be written as
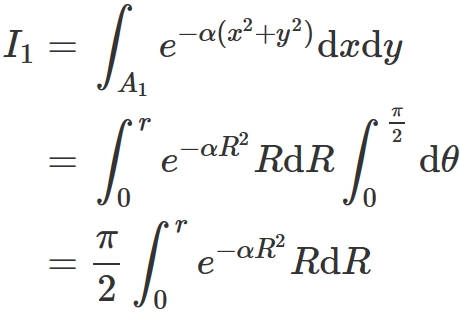 . Here, let $t = R^{2}$. The integral
can be calculated as
. Here, let $t = R^{2}$. The integral
can be calculated as
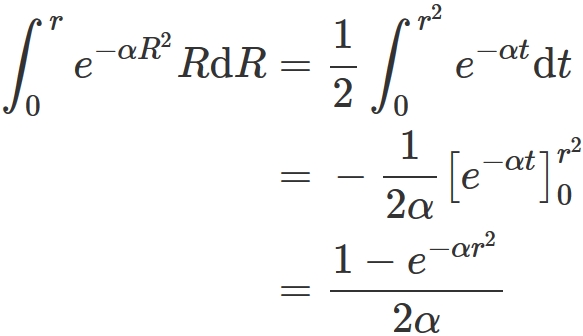 . Hence we obtain
. Hence we obtain
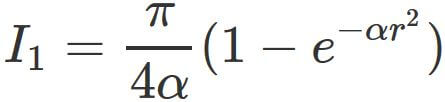 .
.
In the same way as deriving $I_{1}$, we obtain
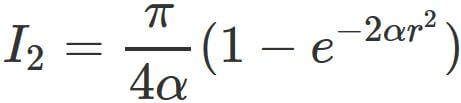 .
The integral $I$ can be written as
.
The integral $I$ can be written as
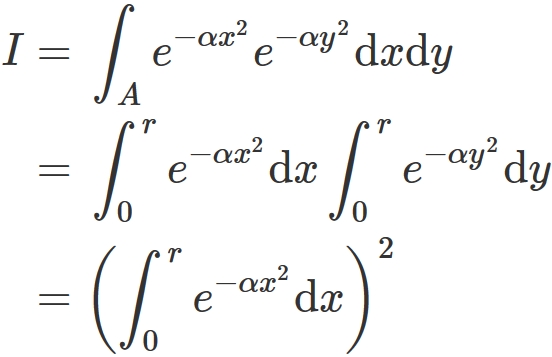 .
From $(1)$, we see that
.
From $(1)$, we see that
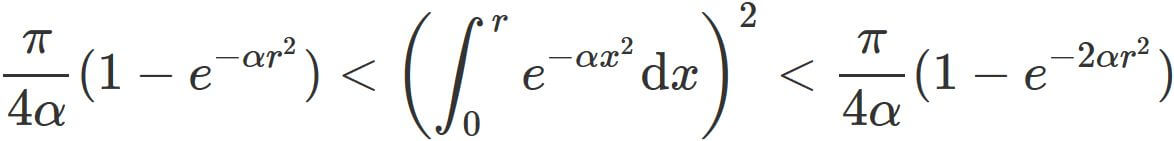 Since the integrand $e^{-\alpha x^{2}}$ is positive,
the integral $\int_{0}^{r} e^{-\alpha x^{2}}\mathrm{d}x$ is positive.
We have
Since the integrand $e^{-\alpha x^{2}}$ is positive,
the integral $\int_{0}^{r} e^{-\alpha x^{2}}\mathrm{d}x$ is positive.
We have
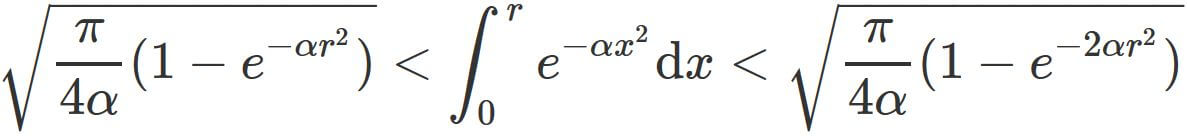 $$
\tag{2}
$$
The limit of the left-hand side as $r$ approaches $+\infty$ is
$$
\tag{2}
$$
The limit of the left-hand side as $r$ approaches $+\infty$ is
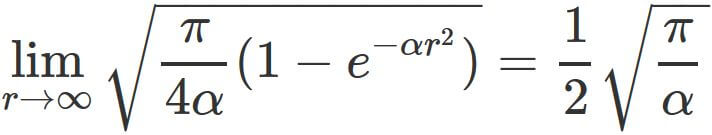 , and the limit of the right-hand side as $r$ approaches $+\infty$ is
, and the limit of the right-hand side as $r$ approaches $+\infty$ is
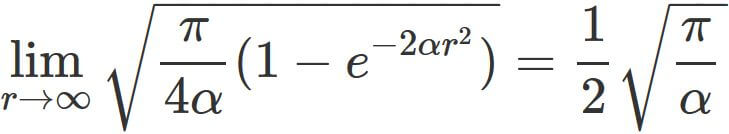 , which is equal to the limit of the left-hand side.
Therefore, by the squeeze theorem and $(2)$, we obtain
, which is equal to the limit of the left-hand side.
Therefore, by the squeeze theorem and $(2)$, we obtain
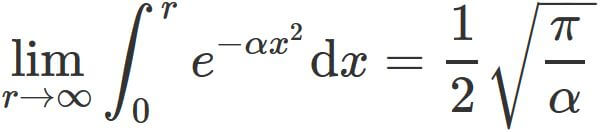 .
This expression is normally expressed as
.
This expression is normally expressed as
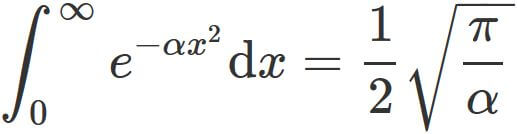 $$
\tag{3}
$$
by omitting the symbol of limit.
$$
\tag{3}
$$
by omitting the symbol of limit.
The Gaussian integral of the range from $-\infty$ to $+\infty$ can be divided as
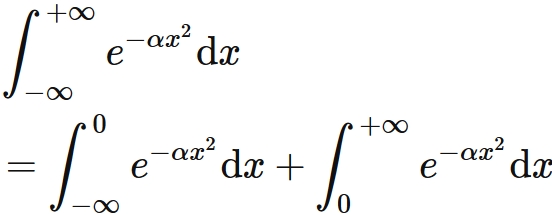 Substituing $(3)$ into this gives
Substituing $(3)$ into this gives
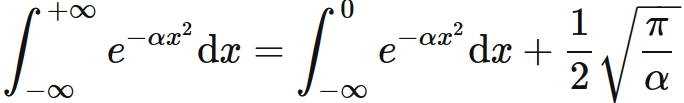 Let $t = -x$, we can calculate the first term by $(2)$ as
Let $t = -x$, we can calculate the first term by $(2)$ as
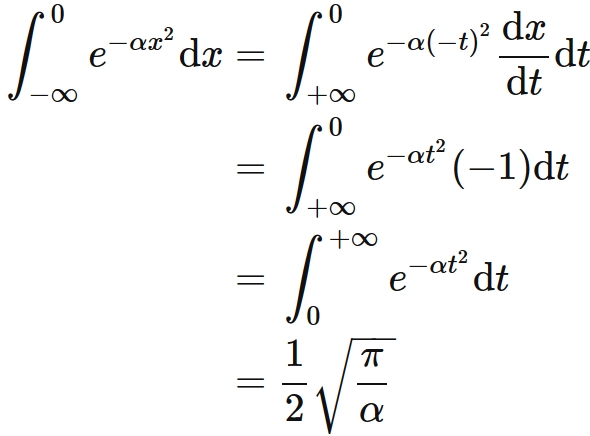
Therefore we obtain
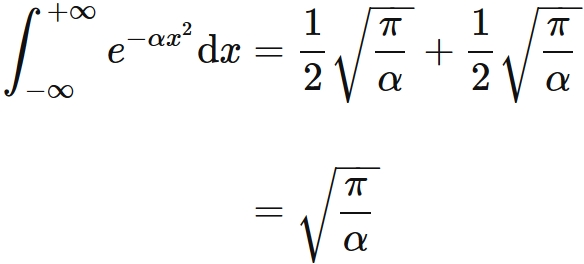
We start with defining three areas in the two dimensional space.
The first area is a closed area $A_{1}$ whose boundary is the x-axis, the y-axis and a circle with radius $r$ centered at the origin.
The second area is a closed area $A$ whose boundary is the x-axis, the y-axis, the line $x=r$, and the line $y=r$. $A$ is a square with an edge length $r$.
The third area is a closed area $A_{2}$ whose boundary is the x-axis, the y-axis and a circle with radius $\sqrt{2}r$ centered at the origin.
In this way, $A_{1}$ is included in $A$ and $A$ is included in $A _ {2}$ (See figure below).

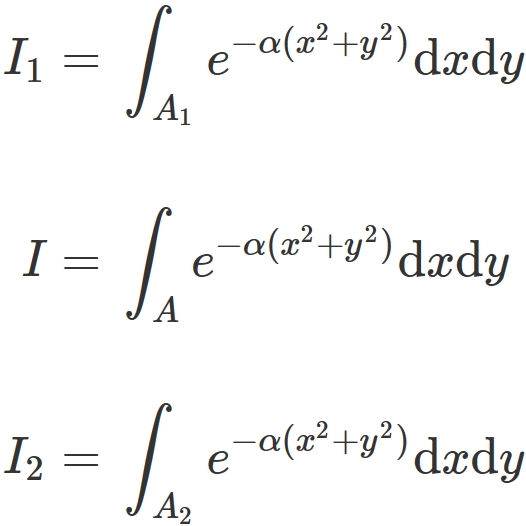
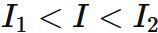
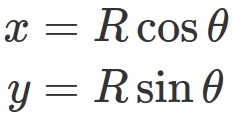
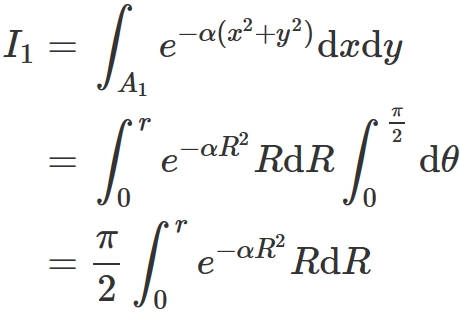
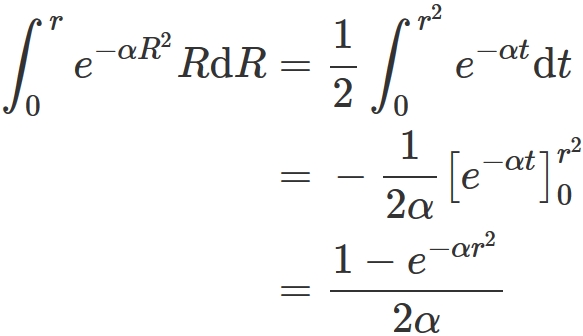
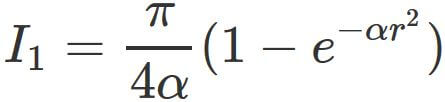
In the same way as deriving $I_{1}$, we obtain
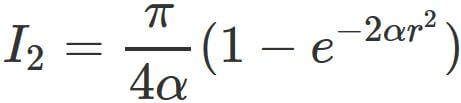
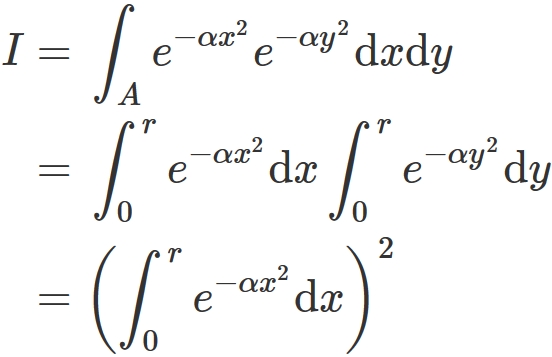
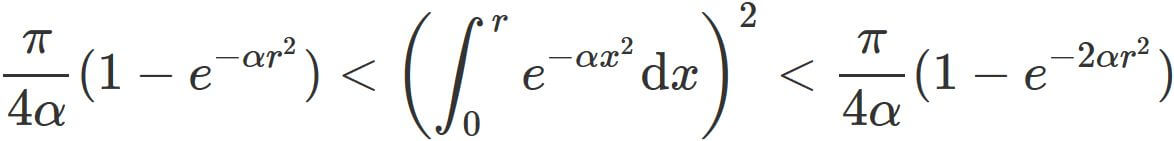
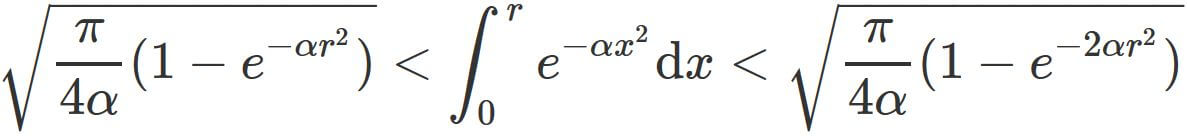
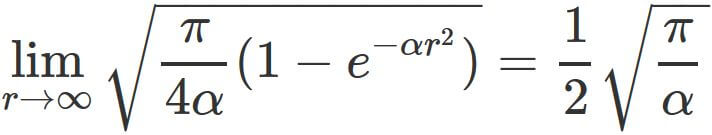
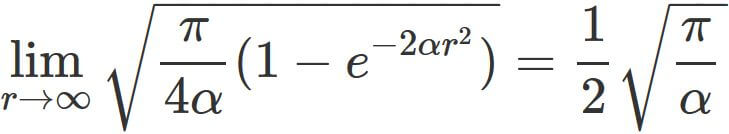
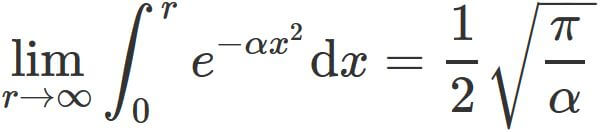
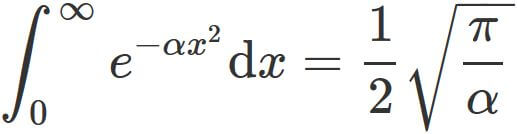
The Gaussian integral of the range from $-\infty$ to $+\infty$ can be divided as
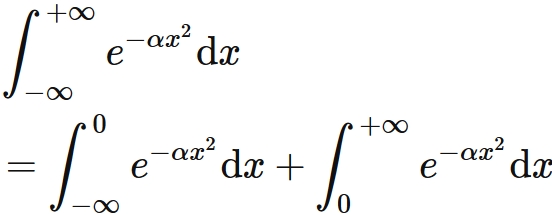
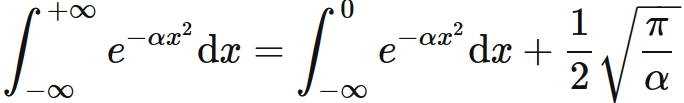
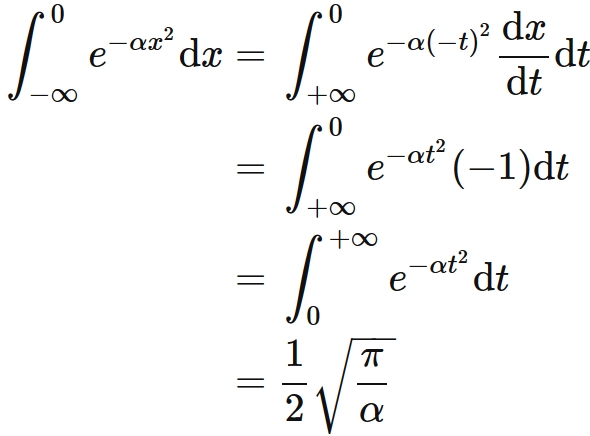
Therefore we obtain
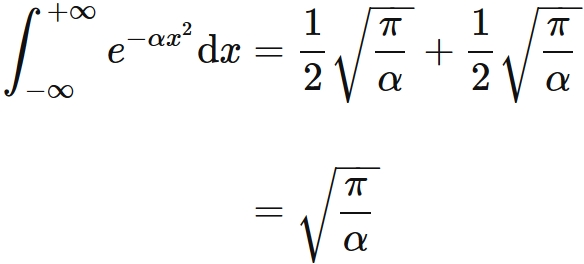

$\int x \exp [- \alpha x^2] \mathrm{d} x$
The following equations hold.
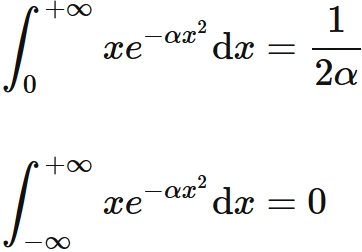
Proof
First, we will prove
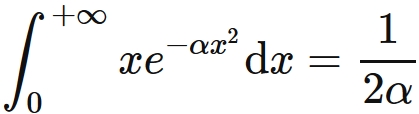 Let $x=\sqrt{t} $, we have
Let $x=\sqrt{t} $, we have
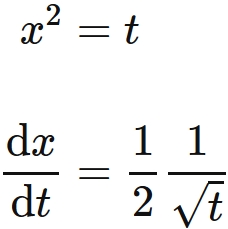 . Using these, we obtain
. Using these, we obtain
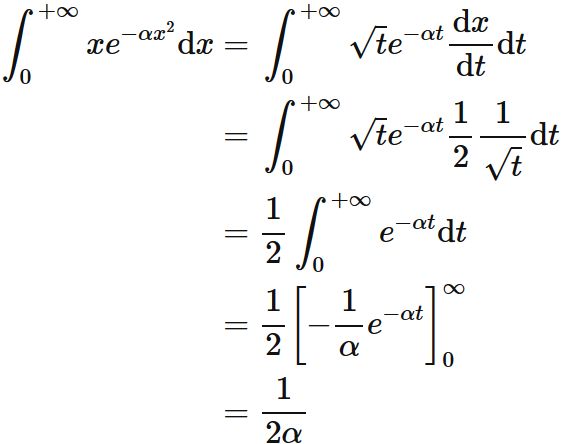 $$
\tag{1}
$$
Next, we will prove
$$
\tag{1}
$$
Next, we will prove
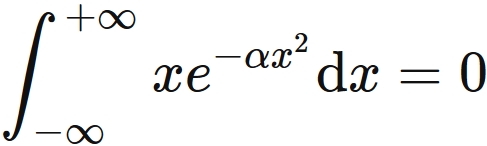 The integral of the range from $-\infty$ to $+\infty$ can be divided as
The integral of the range from $-\infty$ to $+\infty$ can be divided as
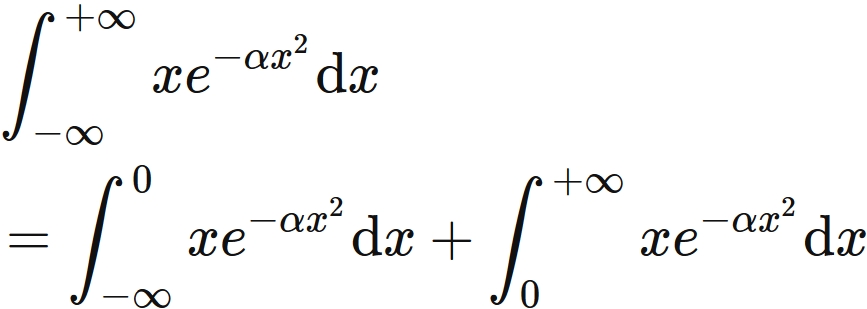 Substituing $(1)$ into this gives
Substituing $(1)$ into this gives
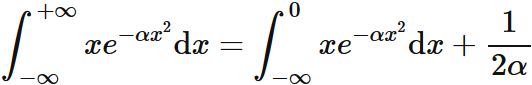 Let $t = -x$, we can calculate the first term by $(1)$ as
Let $t = -x$, we can calculate the first term by $(1)$ as
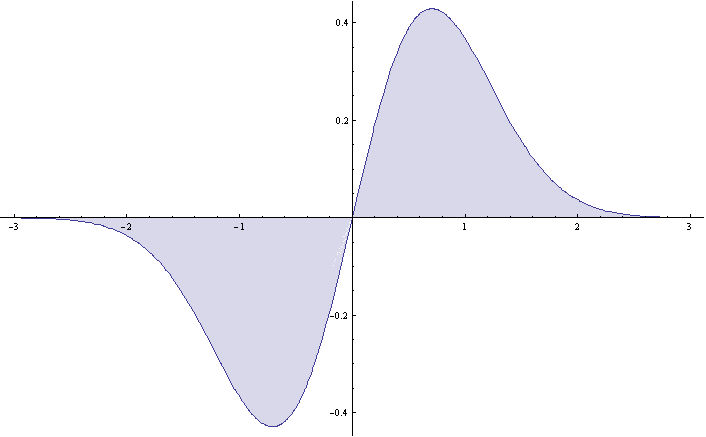
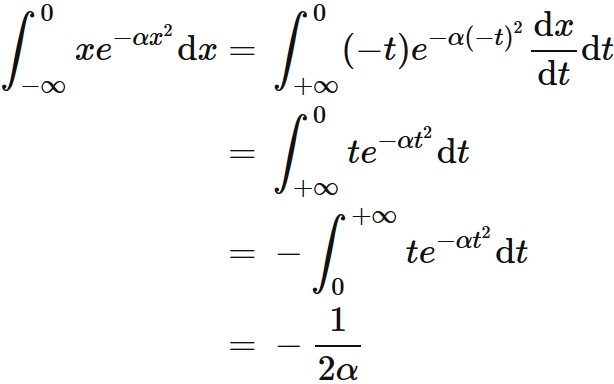 From thise equations, we obtain
From thise equations, we obtain
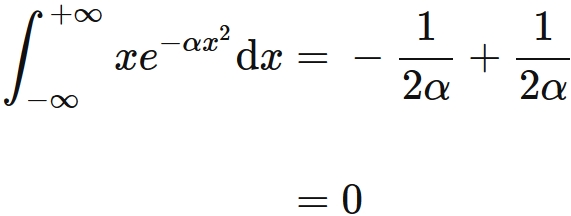
First, we will prove
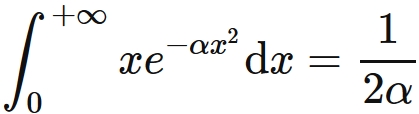
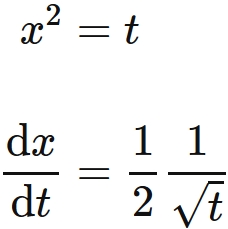
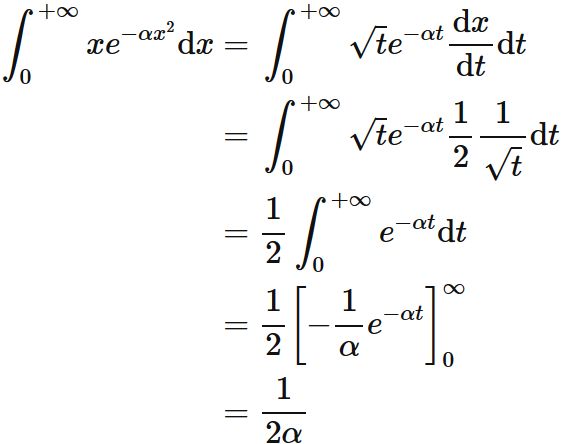
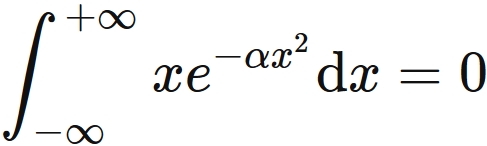
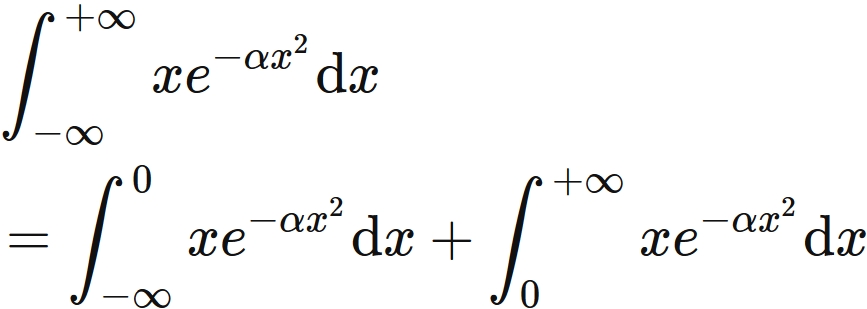
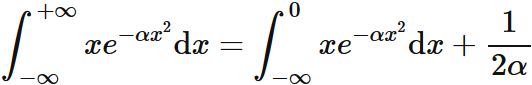
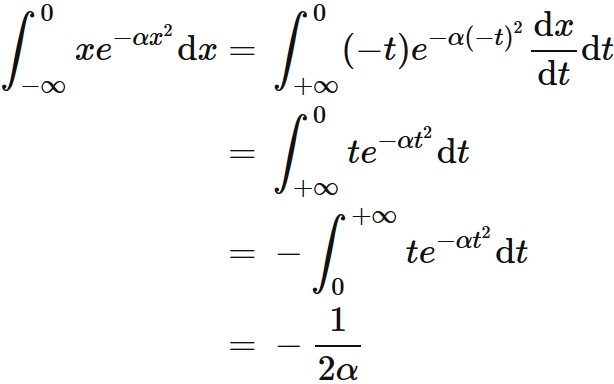
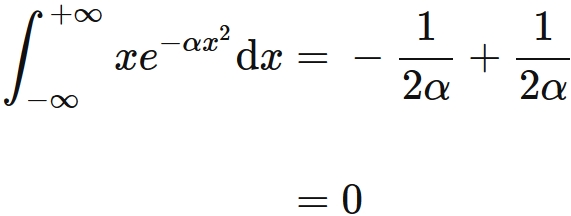

Recurrence formula
Let $I_{n} (\alpha)$ and $J_{n} (\alpha)$ and be integrals defined as
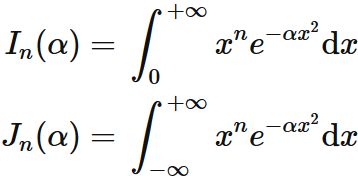
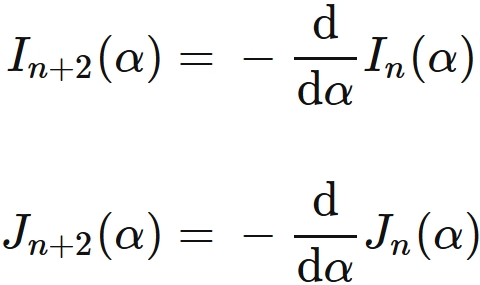
proof
The derivative of $I_{n}(\alpha)$ with respect to $\alpha$ is
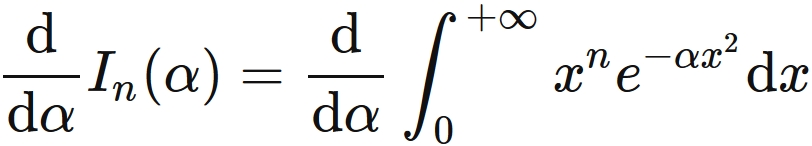 Since the integrand $x^{n} e^{-\alpha x^2}$ and the partial derivative
$
\frac{\mathrm{\partial} }{\mathrm{\partial} \alpha } \left( x^{n} e^{-\alpha x^2} \right)
$
are continuous function, we can commute derivative and integral of the right-hand side.
Since the integrand $x^{n} e^{-\alpha x^2}$ and the partial derivative
$
\frac{\mathrm{\partial} }{\mathrm{\partial} \alpha } \left( x^{n} e^{-\alpha x^2} \right)
$
are continuous function, we can commute derivative and integral of the right-hand side.
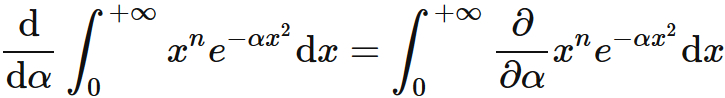 By calculating the derivative, we obtain
By calculating the derivative, we obtain
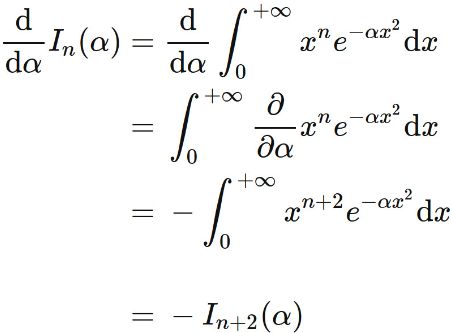 Next, we will prove the recurrence formula for $J_{n}(\alpha)$.
The only difference between
$I_{n}(\alpha)$ and
$J_{n}(\alpha)$ is
the integral range.
We thus apply the same discussion for $I_{n}(\alpha)$, and obtain
Next, we will prove the recurrence formula for $J_{n}(\alpha)$.
The only difference between
$I_{n}(\alpha)$ and
$J_{n}(\alpha)$ is
the integral range.
We thus apply the same discussion for $I_{n}(\alpha)$, and obtain
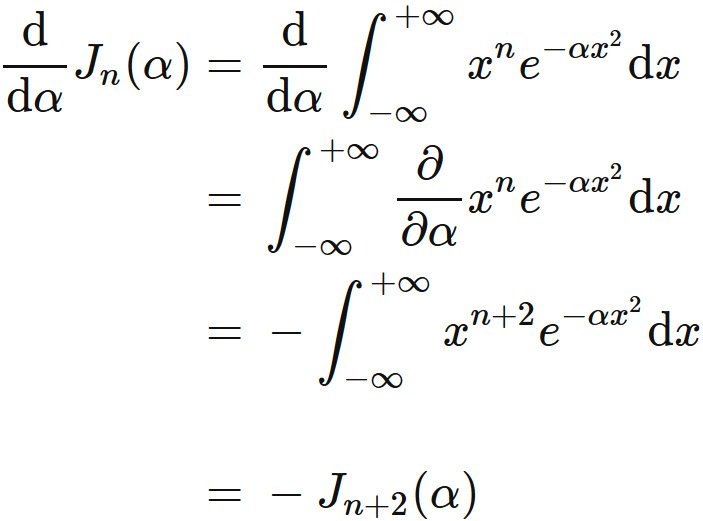
The derivative of $I_{n}(\alpha)$ with respect to $\alpha$ is
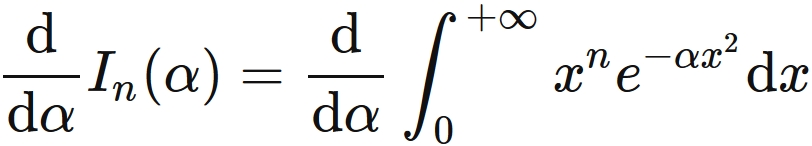
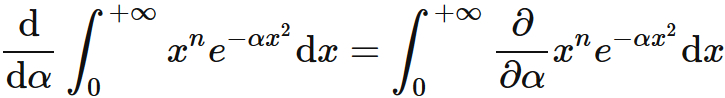
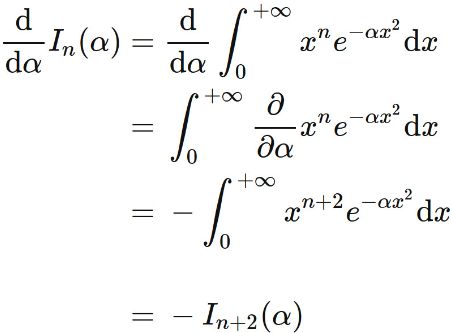
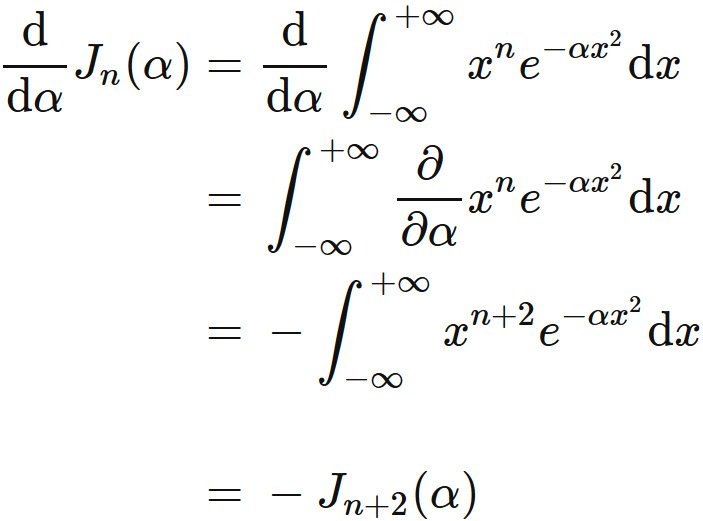
$\int x^2 e^{-\alpha x^2} \mathrm{d}x$
The following equations hold.
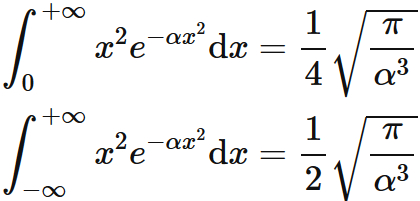
Proof
The recurrence formula for $n=0$ is
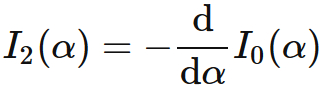 $I_{0}(\alpha)$ is the Gaussian integral :
$I_{0}(\alpha)$ is the Gaussian integral :
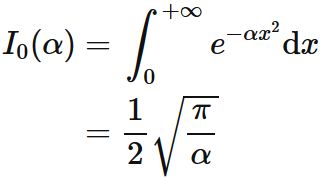 Therefore, we obtain
Therefore, we obtain
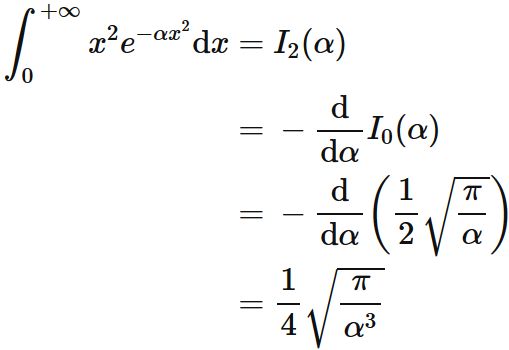 Similarly,
the recurrence formula for $n=0$ is
Similarly,
the recurrence formula for $n=0$ is
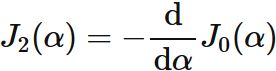 $J_{0}(\alpha)$ is the Gaussian integral :
$J_{0}(\alpha)$ is the Gaussian integral :
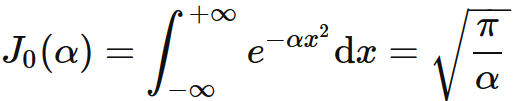 Therefore, we obtain
Therefore, we obtain
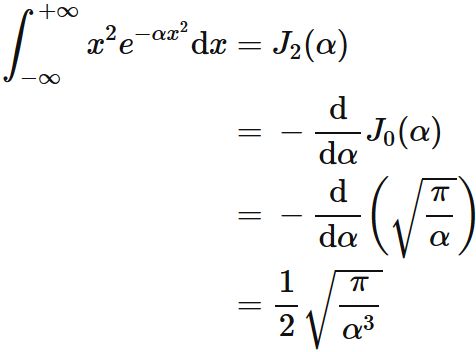
The recurrence formula for $n=0$ is
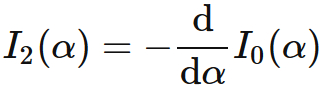
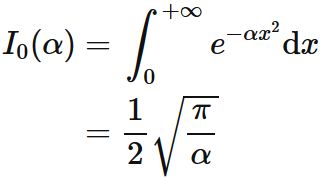
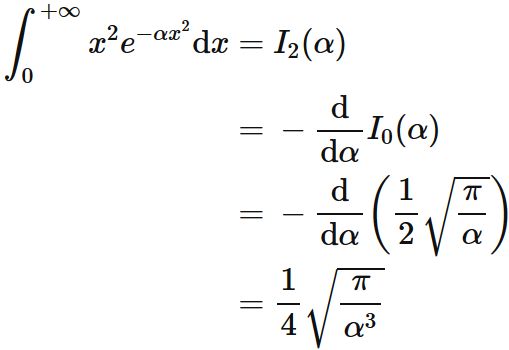
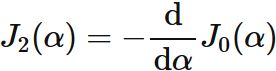
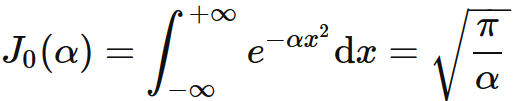
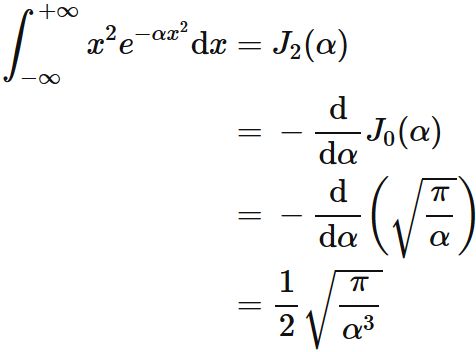

$\int x^3 e^{-\alpha x^2} \mathrm{d}x$
The following equations hold.
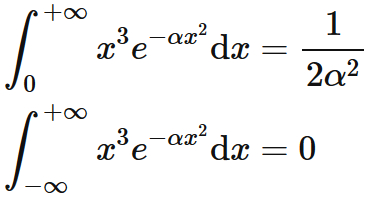
Proof
The recurrence formula for $n=1$ is
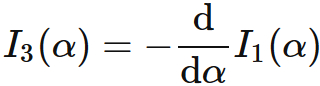 Since
Since
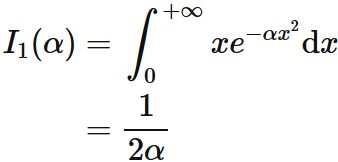 (see $\int x e^{-\alpha x^2} \mathrm{d}x$) ,
we obtain
(see $\int x e^{-\alpha x^2} \mathrm{d}x$) ,
we obtain
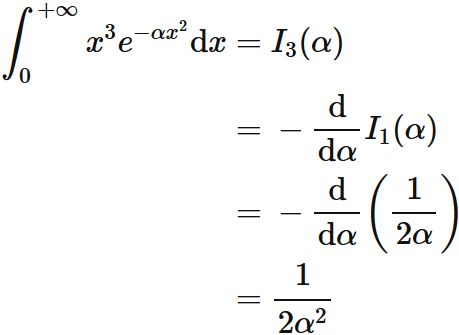
Similarly, the recurrence formula of $J_{n}(\alpha)$ for $n=1$ is
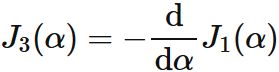 Since
Since
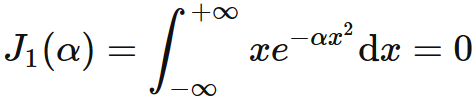 (see $\int x e^{-\alpha x^2} \mathrm{d}x$) , we obtain
(see $\int x e^{-\alpha x^2} \mathrm{d}x$) , we obtain
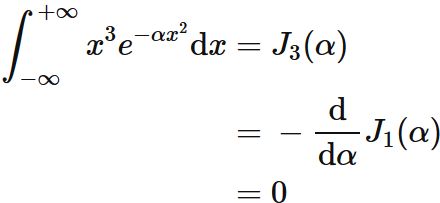
The recurrence formula for $n=1$ is
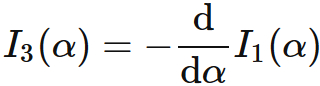
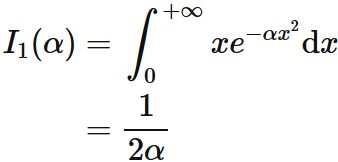
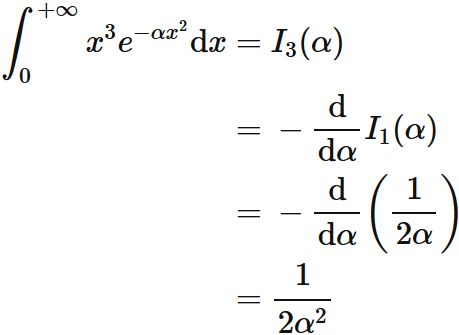
Similarly, the recurrence formula of $J_{n}(\alpha)$ for $n=1$ is
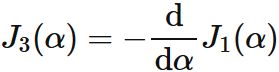
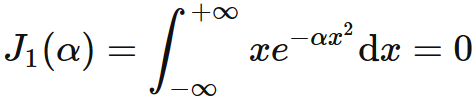
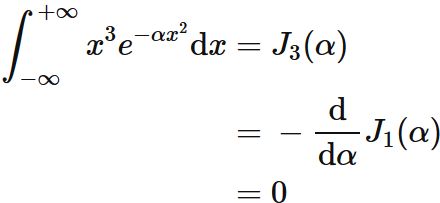

$\int x^4 e^{-\alpha x^2} \mathrm{d}x $
The following equations hold.
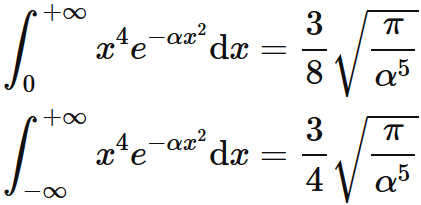
Proof
The recurrence formula for $n=1$ is
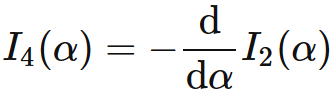 Since
Since
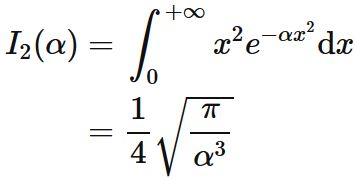 (see $\int x^2 e^{-\alpha x^2} \mathrm{d}x$), we obtain
(see $\int x^2 e^{-\alpha x^2} \mathrm{d}x$), we obtain
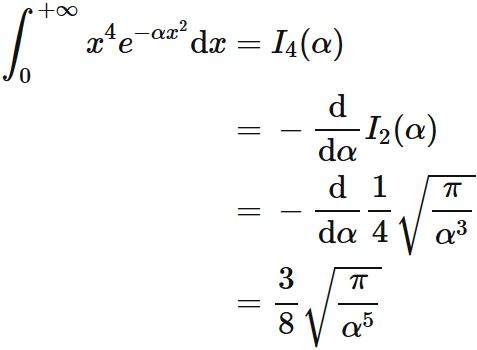 Similarly,
the recurrence formula of $J_{n}(\alpha)$ for $n=2$ is
Similarly,
the recurrence formula of $J_{n}(\alpha)$ for $n=2$ is
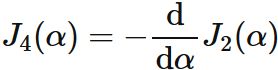 Since
Since
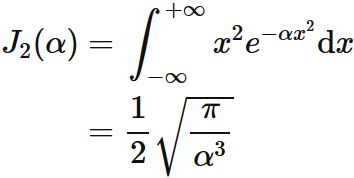 (see $\int x^2 e^{-\alpha x^2} \mathrm{d}x$), we obtain
(see $\int x^2 e^{-\alpha x^2} \mathrm{d}x$), we obtain
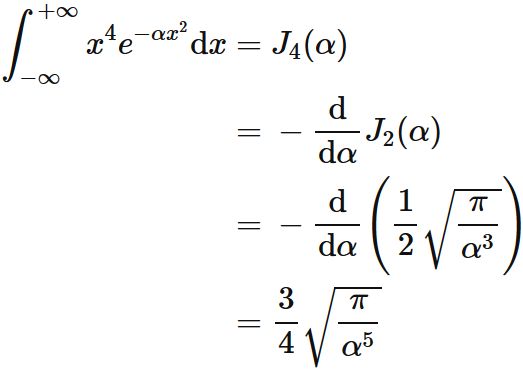
The recurrence formula for $n=1$ is
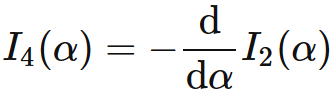
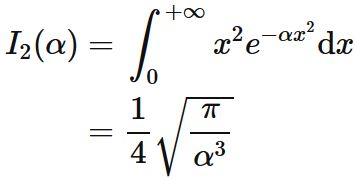
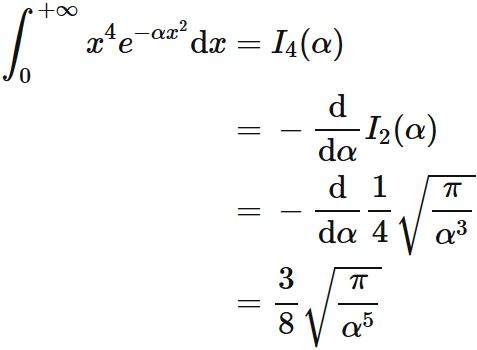
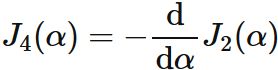
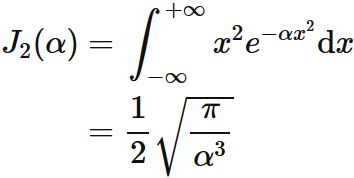
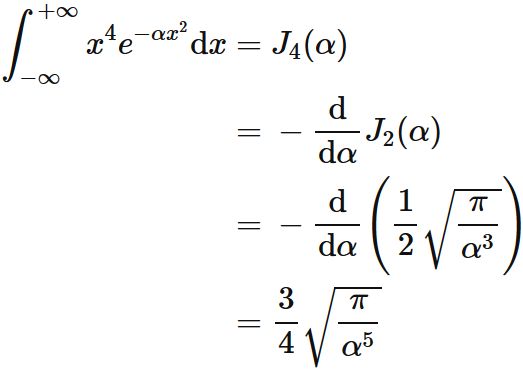

$\int e^{-(a x^2 + bx +c)} \mathrm{d}x$
The following equations hold.
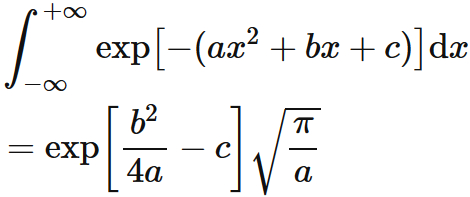
Proof
Completing the square in the exponential gives
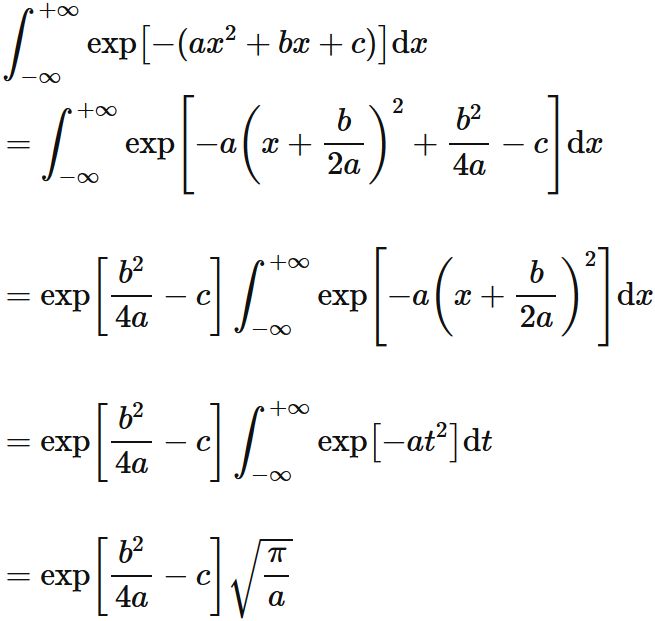 , where we put $t=x + \frac{b}{2a}$ and used the Gaussian integral in the last equality.
, where we put $t=x + \frac{b}{2a}$ and used the Gaussian integral in the last equality.
Completing the square in the exponential gives