Inverse matrix of a 2x2 matrix
Show the inverse matrix of a 2x2 matrix
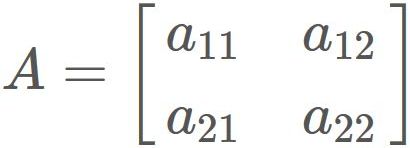
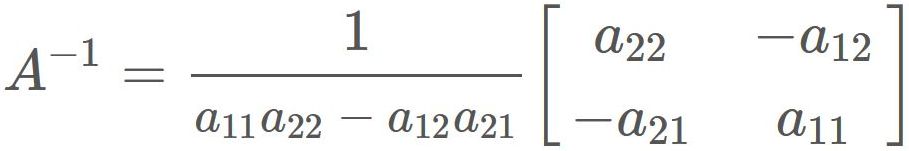
Proof
To find the inverse marix of a 2x2 matrix $A$, we use the property that the inverse matrix is the product of the reciprocal of the determinant and the adjugate matrix, i.e.,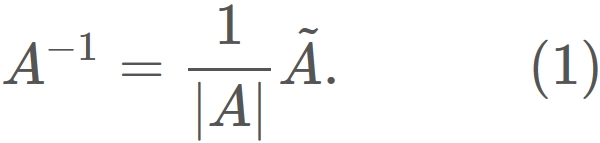
The determinant of $A$ is
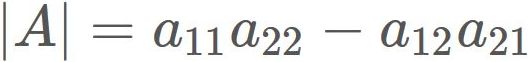
The adjugate matrix $\tilde{A}$ is defined as
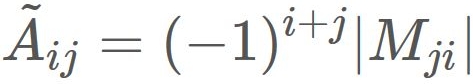
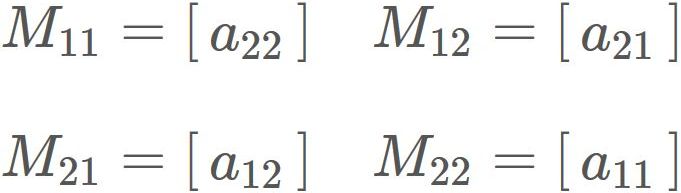
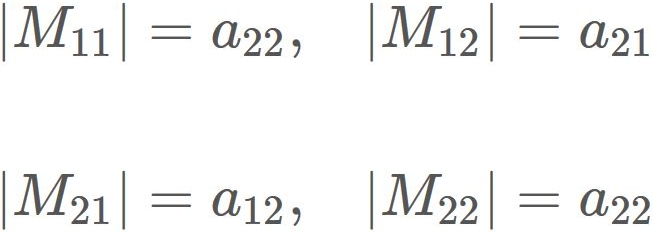
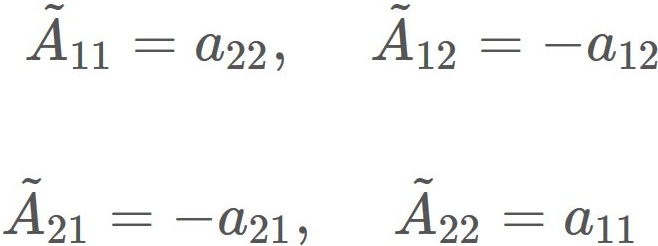
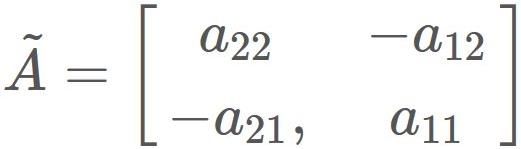
By substituing $|A|$ and $\tilde{A}$ into $(1)$, we obtain
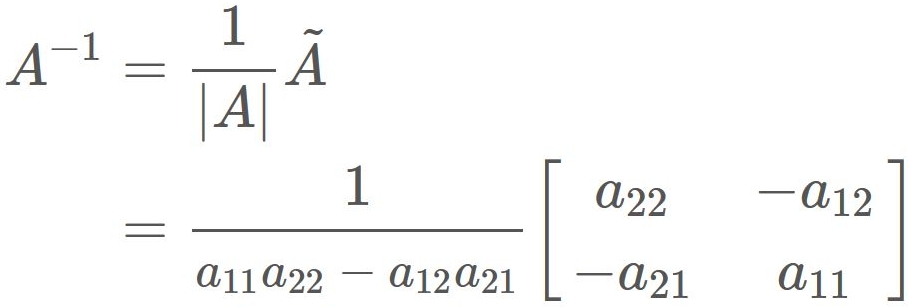
Calculator
Enter a 2x2 matrix and press "Execute" button. Then its inverse matrix is displayed.
Matrix
Inverse matrix
| 1 | 2 | |
| 1 | ||
| 2 |