Examples of Gauss-Jordan elimination
| Table of contents | |
|---|---|
| - | $3 \times 3$ example |
| - | $4 \times 4$ example |
$3 \times 3$ example
Find the inverse matrix of a 3x3 matrix,
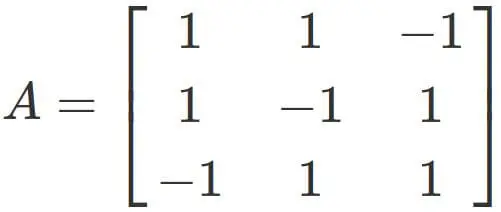
Sample answer
To obtain the inverse matrix, we define a matrix in which the matrix $A$ and the identity matrix $I$ are arranged side by side,
 . This matrix is called augmented matrix.
We transform the matrix $A$ in the augumented matrix to the identity matrix $I$ by performing elementary row operations, i.e.,
. This matrix is called augmented matrix.
We transform the matrix $A$ in the augumented matrix to the identity matrix $I$ by performing elementary row operations, i.e.,
 .
As a result, the identity matrix in the right half of the augmented matrix becomes the inverse of $A$.
This method of finding the inverse matrix is called Gauss-Jordan elimination.
(Here, the dotted line drawn vertically is merely a convenience for distinguishing between the left side and the right side.)
.
As a result, the identity matrix in the right half of the augmented matrix becomes the inverse of $A$.
This method of finding the inverse matrix is called Gauss-Jordan elimination.
(Here, the dotted line drawn vertically is merely a convenience for distinguishing between the left side and the right side.)
According to this method, we perform elementary row operations as follows.
 Therefore, we obtain
Therefore, we obtain

To obtain the inverse matrix, we define a matrix in which the matrix $A$ and the identity matrix $I$ are arranged side by side,


According to this method, we perform elementary row operations as follows.


$4 \times 4$ example
Find the inverse matrix of a 4x4 matrix,

Sample answer
To obtain the inverse matrix, we define a matrix in which the matrix $A$ and the identity matrix $I$ are arranged side by side,
 . This matrix is called augmented matrix.
We transform the matrix $A$ in the augumented matrix to the identity matrix $I$ by performing elementary row operations, i.e.,
. This matrix is called augmented matrix.
We transform the matrix $A$ in the augumented matrix to the identity matrix $I$ by performing elementary row operations, i.e.,
 .
As a result, the identity matrix in the right half of the augmented matrix becomes the inverse of $A$.
This method of finding the inverse matrix is called Gauss-Jordan elimination.
(Here, the dotted line drawn vertically is merely a convenience for distinguishing between the left side and the right side.)
.
As a result, the identity matrix in the right half of the augmented matrix becomes the inverse of $A$.
This method of finding the inverse matrix is called Gauss-Jordan elimination.
(Here, the dotted line drawn vertically is merely a convenience for distinguishing between the left side and the right side.)
According to this method, we perform elementary row operations as follows.
 Therefore,
we obtain
Therefore,
we obtain

To obtain the inverse matrix, we define a matrix in which the matrix $A$ and the identity matrix $I$ are arranged side by side,


According to this method, we perform elementary row operations as follows.

