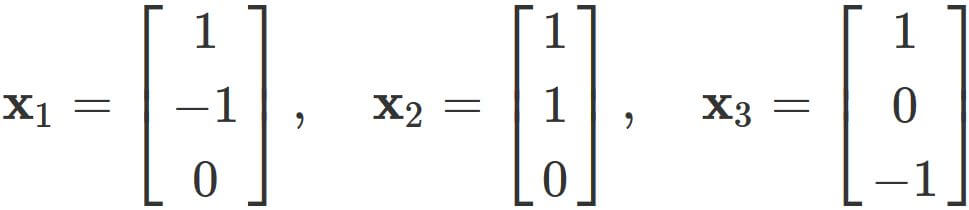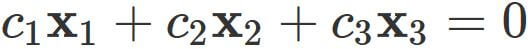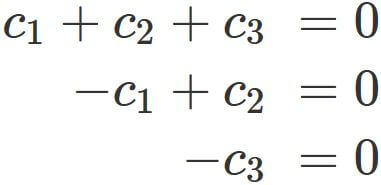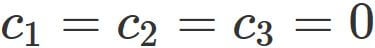Definition of linear independence/dependence and examples
A set of $n$ vectors $\{ \mathbf{x}_{1}, \mathbf{x}_{2}, \cdots, \mathbf{x}_{n} \}$ is said to be linearly independent iff the equation
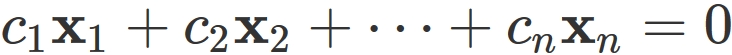

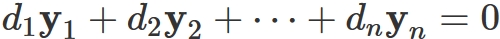
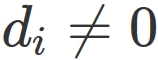
Below are a brief supplement and examples.
Explanation
Acoording to the above definition, if a set of vectors $\{ \mathbf{y}_{1}, \mathbf{y}_{2}, \cdots, \mathbf{y}_{n} \}$ is linearly dependent, at least one vector in the vectors can be represented by a linear combination of the remaining vectors. For example, if $d_{i} \neq 0$, $\mathbf{y}_{i}$ can be represented as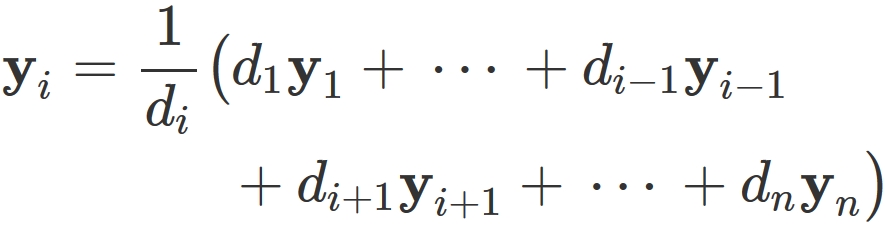
Therefore, a set of vectors is said to be linearly dependent when at least one vector in the vectors can be represented by a linear combination of the remaining vectors. On the other hand, a set of vectors is said to be linearly independent when any vector can not be represented by a linear combination of the remaining vectors.
Example 1:
A set of vectors
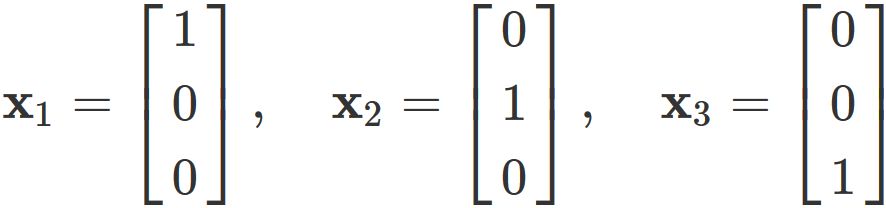
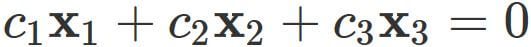
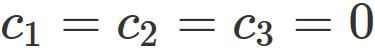
Example 2:
Let us investigate whether
a set of vectors
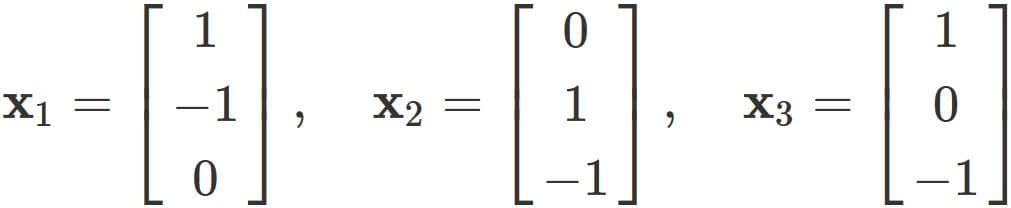
If the equation
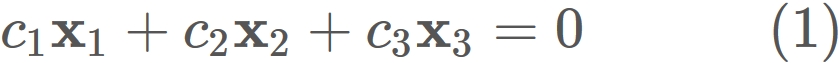
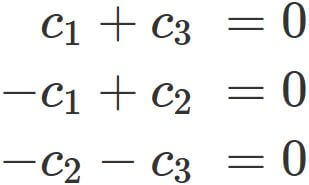
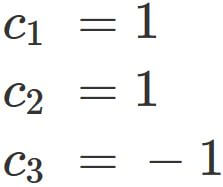
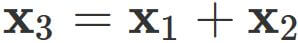
Example 3:
Let us investigate a set of vectors