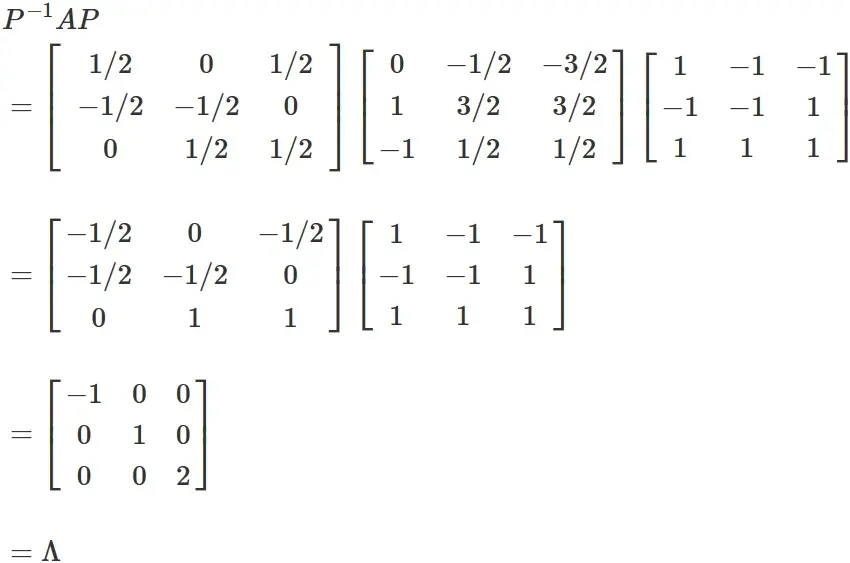Examples: matrix diagonalization
| 2x2 matrix | |
|---|---|
| - | Matrix diagonalization |
| - | Invertible matrix to diagonalize |
| - | Check diagonalization |
| 3x3 matrix | |
|---|---|
| - | Matrix diagonalization |
| - | Invertible matrix to diagonalize |
| - | Check diagonalization |
$2 \times 2$ matrix diagonalization
Let $A$ be a $2 \times 2$ matrix defined as
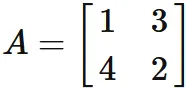
Answer
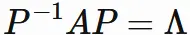 , where $P$ is an invertible matrix which diagonalizes $A$.
, where $P$ is an invertible matrix which diagonalizes $A$.
In the following, we find the diagonal matrix $\Lambda$ for the matrix $A$ in $(1.1)$, and the invertive matrix $P$ that diagonalizes $A$. It is known that the diagonal elements of a diagonalized matrix are the eigenvalues of the original matrix. Therefore, by obtaining eigenvalues of $A$ and arranging them in diagonal elements, diagonalized matrix $\Lambda$ is obtained.
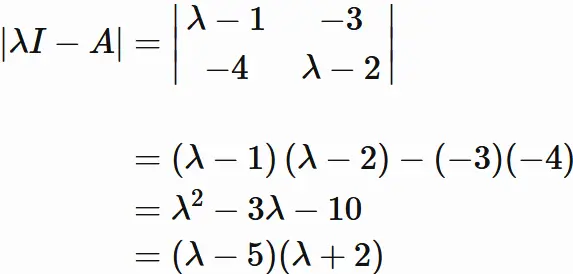 Then the solutions of
$(1.2)$ are
Then the solutions of
$(1.2)$ are
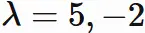 By arranging these solutions in diagonal elements,
we obtain the diagonalized matrix $\Lambda$ as
By arranging these solutions in diagonal elements,
we obtain the diagonalized matrix $\Lambda$ as
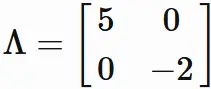 $$
\tag{1.3}
$$
$$
\tag{1.3}
$$
Case $\lambda=5$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
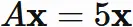 Let $\mathbf{x}$ be
Let $\mathbf{x}$ be
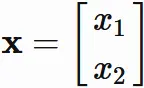 We have
We have
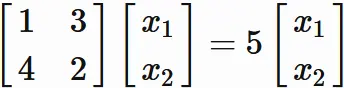 Rearranging this equation,
we obtain
Rearranging this equation,
we obtain
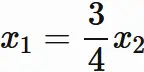 Therefore, the eigenvector is expressed as
Therefore, the eigenvector is expressed as
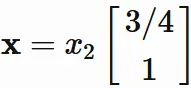 ,
where $x_{2}$ is an arbitrary value.
We set $x_2=1$ for convenience,
and obtain
,
where $x_{2}$ is an arbitrary value.
We set $x_2=1$ for convenience,
and obtain
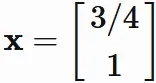 $$
\tag{1.4}
$$
$$
\tag{1.4}
$$
Case $\lambda=-2$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
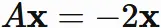 Let $\mathbf{x}$ be
Let $\mathbf{x}$ be
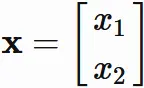 We have
We have
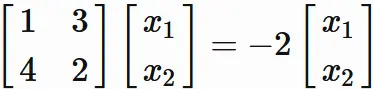 Rearranging this equation, we obtain
Rearranging this equation, we obtain
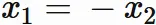 Therefore, the eigenvector is expressed as
Therefore, the eigenvector is expressed as
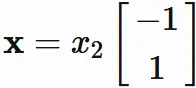 where $x_2$ is an arbitrary value.
We set $x_2=1$ for convenience, and obtain
where $x_2$ is an arbitrary value.
We set $x_2=1$ for convenience, and obtain
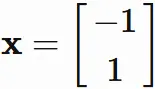 $$
\tag{1.5}
$$
$$
\tag{1.5}
$$
Invertible matrix $P$
By $(1.4)$ and $(1.5)$, we obtain the invertible matrix $P$ as
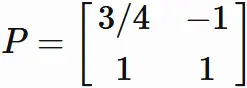 $$
\tag{1.6}
$$
$$
\tag{1.6}
$$
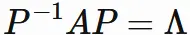 To do that,
we need to derive the inverse matrix $P^{−1}$.
To do that,
we need to derive the inverse matrix $P^{−1}$.
Derivation of $P^{-1}$
We will derive the inverse matrix $P^{−1}$ by Gaussian elimination. We define a matrix in which $P$ and the identity matrix $I$ are arranged side by side,
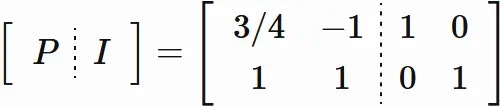 $$
\tag{1.7}
$$
and tramsform the left half matrix
to the identity matrix
by the elementary row operations:
$$
\tag{1.7}
$$
and tramsform the left half matrix
to the identity matrix
by the elementary row operations:
 As a result,
the matrix appearing in the right half
becomes the inverse matrix $P^{−1}$.
According to this method,
performing the elementary row operations
to the matrix $(1.7)$, we have
As a result,
the matrix appearing in the right half
becomes the inverse matrix $P^{−1}$.
According to this method,
performing the elementary row operations
to the matrix $(1.7)$, we have
 Therere we obtain
Therere we obtain
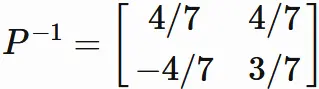
Check diagonalization
Now we can check the diagonalization as follows.
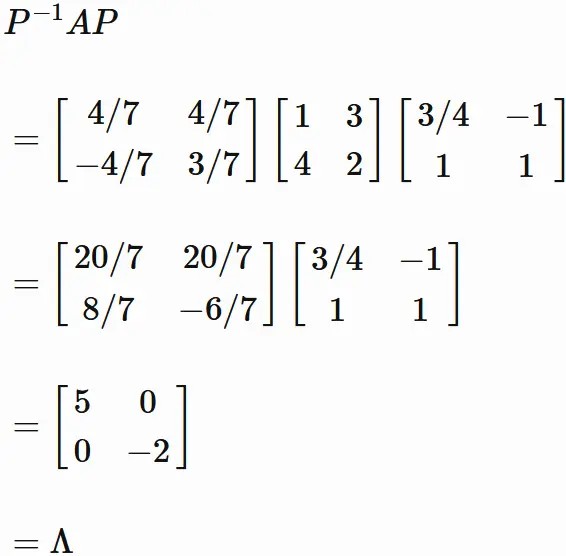 We see that
$P$ diagonalizes $A$.
We see that
$P$ diagonalizes $A$.
● Preparation
For a square matrix $A$,
matrix diagonalization is to find a diagonal matrix $\Lambda$ satisfying
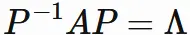
In the following, we find the diagonal matrix $\Lambda$ for the matrix $A$ in $(1.1)$, and the invertive matrix $P$ that diagonalizes $A$. It is known that the diagonal elements of a diagonalized matrix are the eigenvalues of the original matrix. Therefore, by obtaining eigenvalues of $A$ and arranging them in diagonal elements, diagonalized matrix $\Lambda$ is obtained.
●
Derivation of diagonal matrix $\Lambda$
In order to obtain the eigenvalue $\Lambda$ of $A$,
we need to solve the characteristic equation
\begin{eqnarray}
\left| \lambda I - A \right| = 0
\end{eqnarray}
$$
\tag{1.2}
$$
, which is a polynomial equation in the variable (eigenvalue) $\lambda$.
Since the left-hand side is a
$2 \times 2$ determinant,
we have
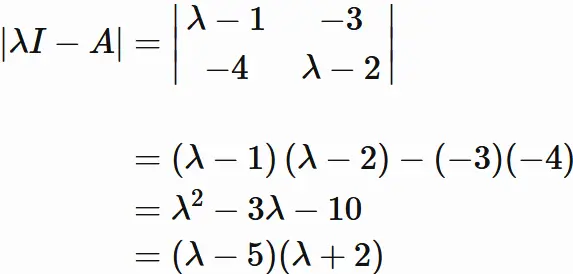
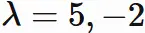
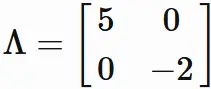
●
Derivation of invertible matrix that diagonalizes $A$
The invertible matrix $P$
diagonalizing the matrix $A$
is the matrix whose columun vectors are the eigenvectors of $A$.
Therefore, $P$ is obtained,
if the eigenvector for each eigenvalue of $A$ is obtained.
So, we will derive the eigenvectors of the eigenvalues of $A$ as follows.
Case $\lambda=5$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
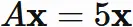
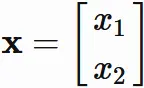
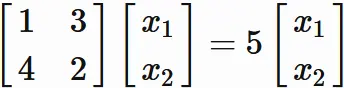
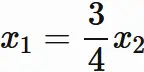
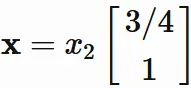
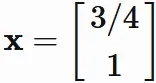
Case $\lambda=-2$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
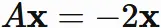
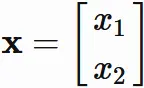
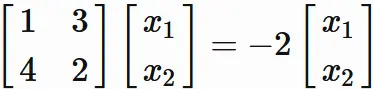
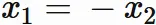
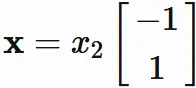
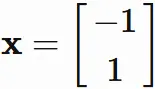
Invertible matrix $P$
By $(1.4)$ and $(1.5)$, we obtain the invertible matrix $P$ as
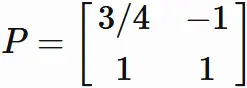
● Check the answer
We will check
whether the matrix $P$ in equation $(1.6)$
actually diagonalizes the matrix $A$,
that is, whether $P$, $A$ and $\Lambda$ satisfy
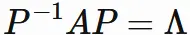
Derivation of $P^{-1}$
We will derive the inverse matrix $P^{−1}$ by Gaussian elimination. We define a matrix in which $P$ and the identity matrix $I$ are arranged side by side,
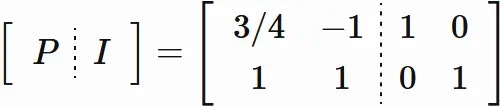


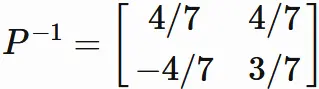
Check diagonalization
Now we can check the diagonalization as follows.
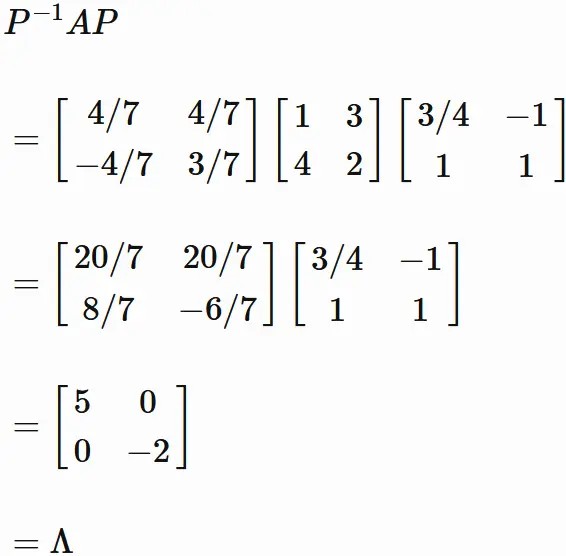
$3 \times 3$ matrix diagonalization
Let $A$ be a $3 \times 3$ matrix defined as
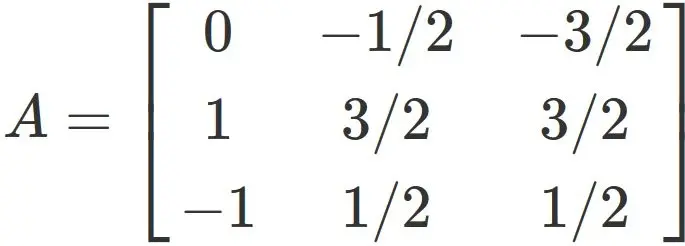
Answer
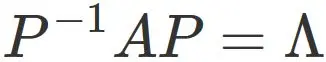 , where $P$ is an invertible matrix which diagonalizes $A$.
, where $P$ is an invertible matrix which diagonalizes $A$.
In the following, we find the diagonal matrix $\Lambda$ for the matrix $A$ in $(2.1)$, and the invertive matrix $P$ that diagonalizes $A$. It is known that the diagonal elements of a diagonalized matrix are the eigenvalues of the original matrix. Therefore, by obtaining eigenvalues of $A$ and arranging them in diagonal elements, diagonalized matrix $\Lambda$ is obtained.
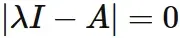 $$
\tag{2.2}
$$
, which is a polynomial equation in the variable (eigenvalue) $\lambda$.
Since the left-hand side is a
$3 \times 3$ determinant,
we have
$$
\tag{2.2}
$$
, which is a polynomial equation in the variable (eigenvalue) $\lambda$.
Since the left-hand side is a
$3 \times 3$ determinant,
we have
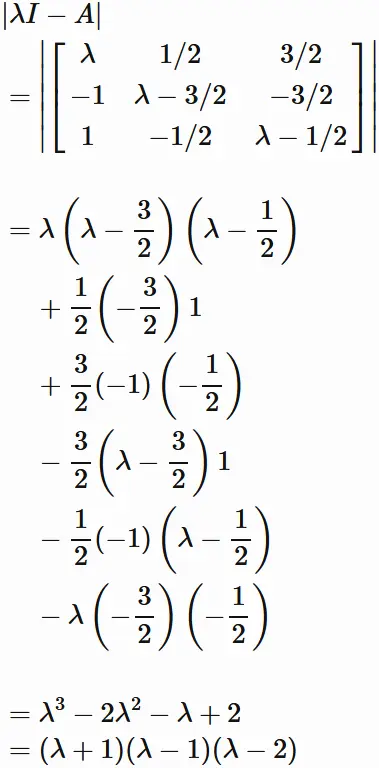 Then the solutions of $(2.2)$ are
Then the solutions of $(2.2)$ are
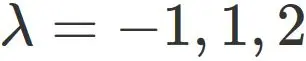 By arranging these solutions in diagonal elements,
we obtain the diagonalized matrix $\Lambda$ as
By arranging these solutions in diagonal elements,
we obtain the diagonalized matrix $\Lambda$ as
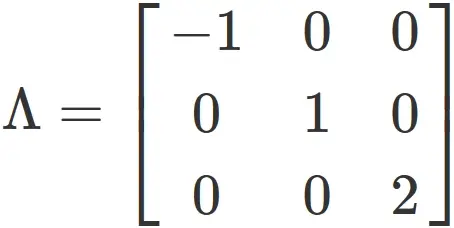 $$
\tag{2.3}
$$
$$
\tag{2.3}
$$
Case $\lambda=-1$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
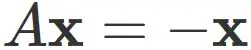 Let $\mathbf{x}$ be
Let $\mathbf{x}$ be
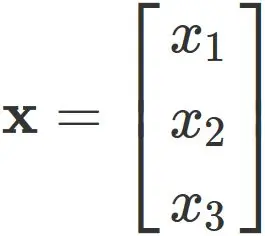 We have
We have
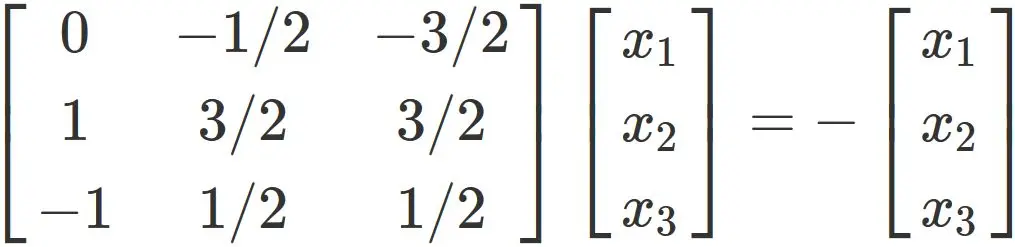 Rearranging this equation, we obtain
Rearranging this equation, we obtain
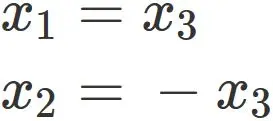 Therefore the eigenvector is expressed as
Therefore the eigenvector is expressed as
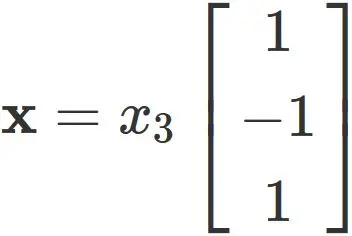 , where $x_{3}$ is an arbitrary value.
Here, we set $ x_ {3} = 1 $ for convenience, and obtain
, where $x_{3}$ is an arbitrary value.
Here, we set $ x_ {3} = 1 $ for convenience, and obtain
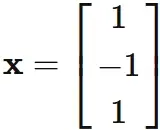 $$
\tag{2.4}
$$
$$
\tag{2.4}
$$
Case $\lambda=1$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
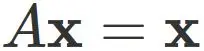 Let $\mathbf{x}$ be
Let $\mathbf{x}$ be
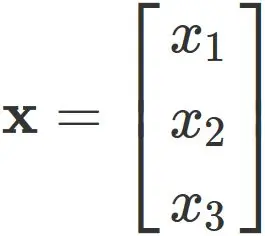 We have
We have
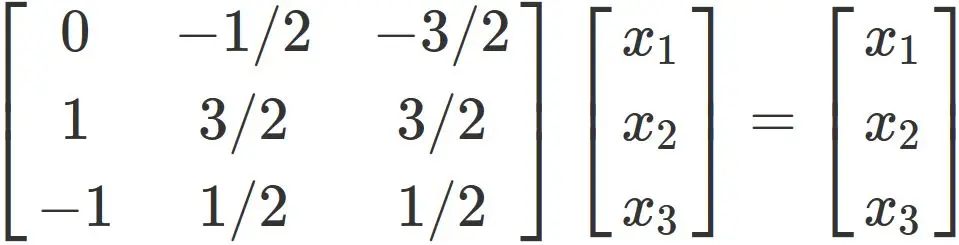 Rearranging this equation, we obtain
Rearranging this equation, we obtain
 Therefore the eigenvector is expressed as
Therefore the eigenvector is expressed as
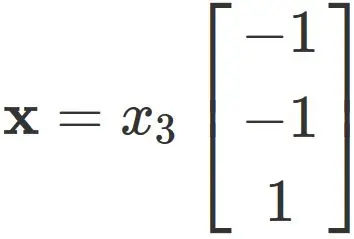 , where $x_{3}$ is an arbitrary value.
Here, we set $ x_ {3} = 1 $ for convenience, and obtain
, where $x_{3}$ is an arbitrary value.
Here, we set $ x_ {3} = 1 $ for convenience, and obtain
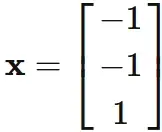 $$
\tag{2.5}
$$
$$
\tag{2.5}
$$
Case $\lambda=2$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
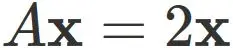 Let $\mathbf{x}$ be
Let $\mathbf{x}$ be
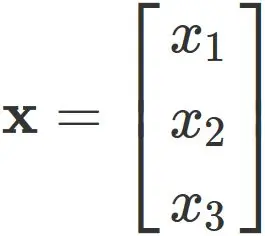 We have
We have
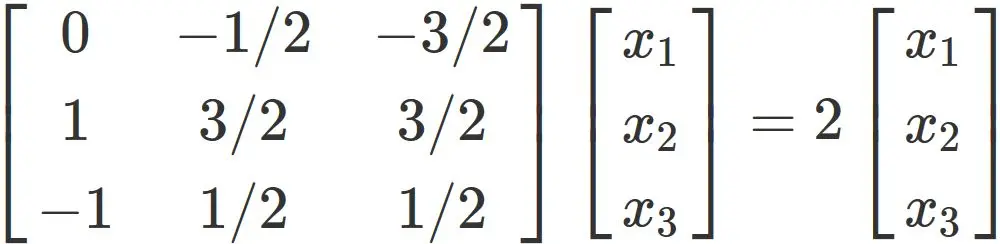 Rearranging this equation, we obtain
Rearranging this equation, we obtain
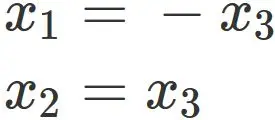 Therefore the eigenvector is expressed as
Therefore the eigenvector is expressed as
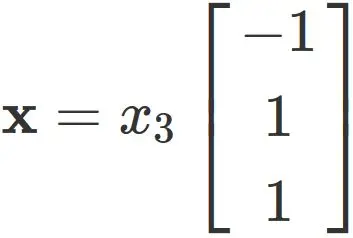 , where $x_{3}$ is an arbitrary value.
Here, we set $ x_ {3} = 1 $ for convenience, and obtain
, where $x_{3}$ is an arbitrary value.
Here, we set $ x_ {3} = 1 $ for convenience, and obtain
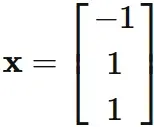 $$
\tag{2.6}
$$
Invertible matrix $P$
$$
\tag{2.6}
$$
Invertible matrix $P$
By (2.4), (2.5) and (2.6), we obtain the invertible matrix $P$ as
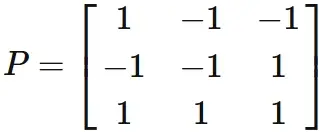 $$
\tag{2.7}
$$
$$
\tag{2.7}
$$
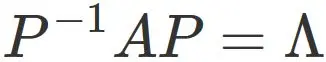 To do that,
we need to derive the inverse matrix $P^{−1}$.
To do that,
we need to derive the inverse matrix $P^{−1}$.
Derivation of $P^{-1}$
We will derive the inverse matrix $P^{−1}$ by Gaussian elimination. We define a matrix in which $P$ and the identity matrix $I$ are arranged side by side,
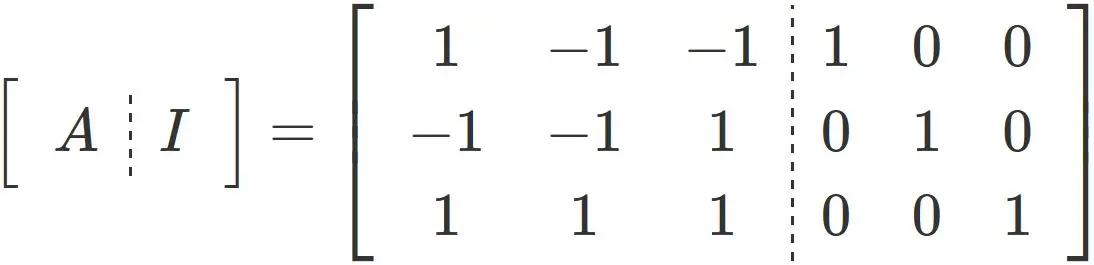 $$
\tag{2.8}
$$
and tramsform
the left half matrix to the identity matrix
by the elementary row operations:
$$
\tag{2.8}
$$
and tramsform
the left half matrix to the identity matrix
by the elementary row operations:
 As a result,
the matrix appearing in the right half
becomes the inverse matrix $A^{−1}$.
According to this method,
performing the elementary row operations to the matrix $(2.8)$,
we have
As a result,
the matrix appearing in the right half
becomes the inverse matrix $A^{−1}$.
According to this method,
performing the elementary row operations to the matrix $(2.8)$,
we have
 Therere we obtain
Therere we obtain
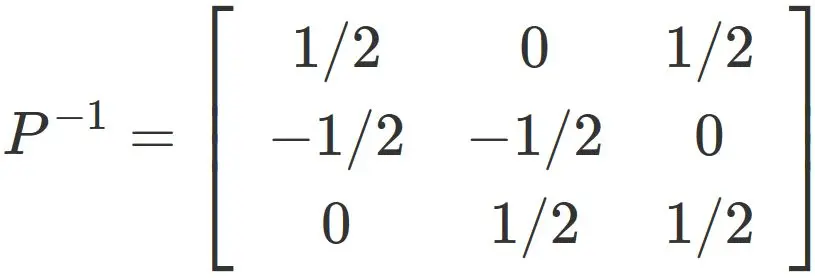
Check diagonalization
Now we can check the diagonalization as follows.
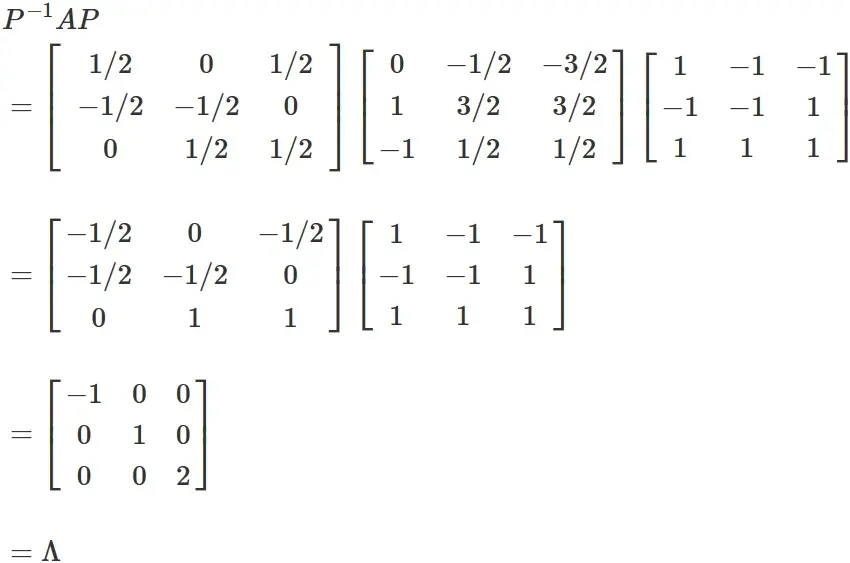 We see that $P$ diagonalizes $A$.
We see that $P$ diagonalizes $A$.
● Preparation
For a square matrix $A$,
matrix diagonalization is to find a diagonal matrix $\Lambda$ satisfying
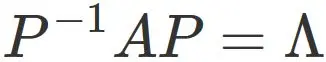
In the following, we find the diagonal matrix $\Lambda$ for the matrix $A$ in $(2.1)$, and the invertive matrix $P$ that diagonalizes $A$. It is known that the diagonal elements of a diagonalized matrix are the eigenvalues of the original matrix. Therefore, by obtaining eigenvalues of $A$ and arranging them in diagonal elements, diagonalized matrix $\Lambda$ is obtained.
●
Derivation of diagonal matrix $\Lambda$
In order to obtain the eigenvalue $\Lambda$ of $A$,
we need to solve the characteristic equation
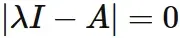
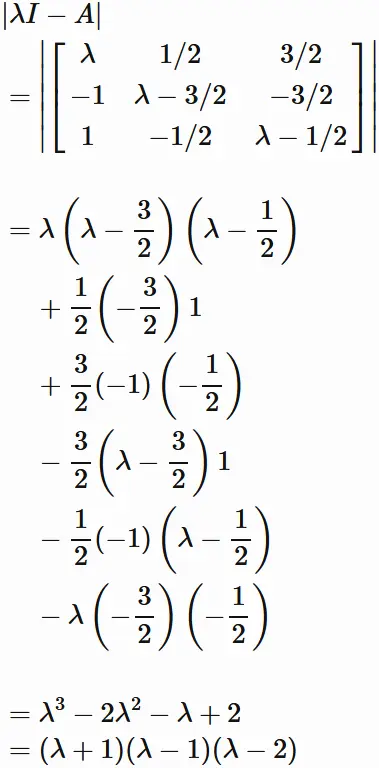
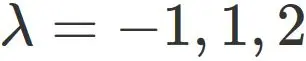
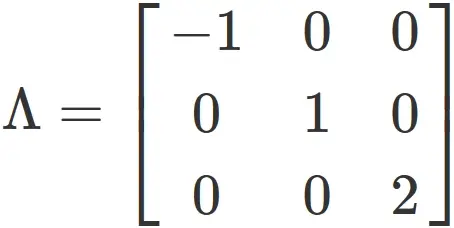
●
Derivation of invertible matrix that diagonalizes $A$
The invertible matrix $P$ that
diagonalizes the matrix $A$
is the matrix whose columun vectors are the eigenvectors of $A$.
Therefore, $P$ is obtained,
if the eigenvector for each eigenvalue of $A$ is obtained.
So, we will derive the eigenvectors of the eigenvalues of $A$ as follows.
Case $\lambda=-1$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
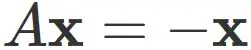
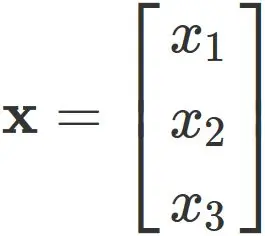
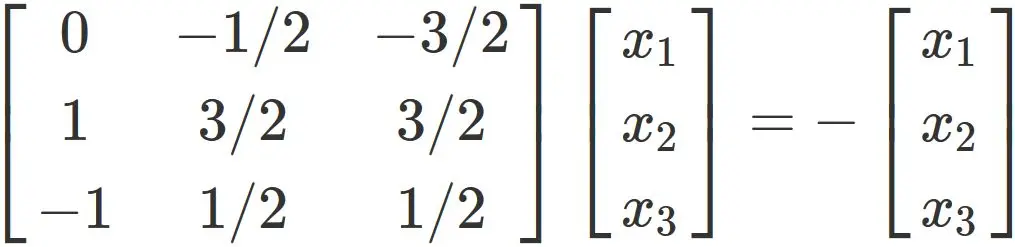
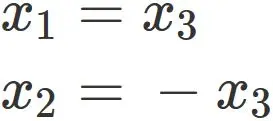
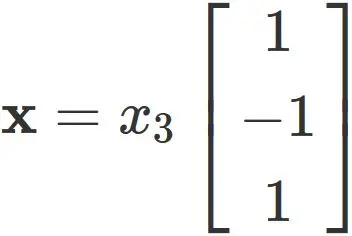
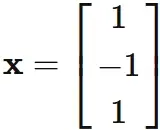
Case $\lambda=1$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
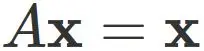
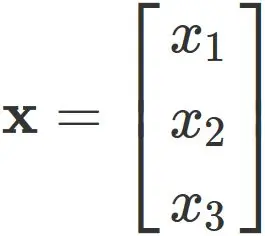
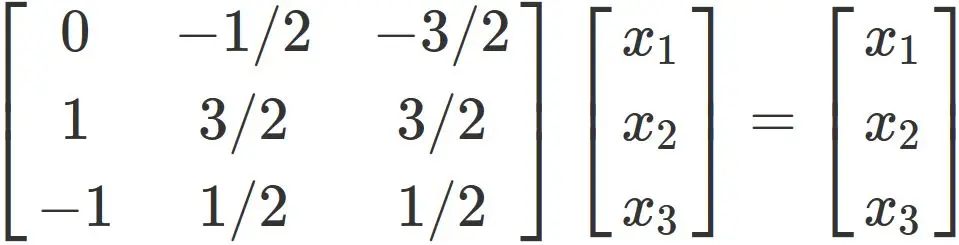

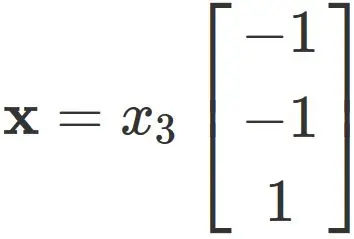
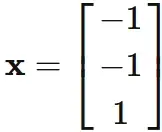
Case $\lambda=2$ :
In this case, the eigenvector $\mathbf{x}$ satisfies
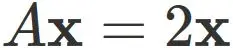
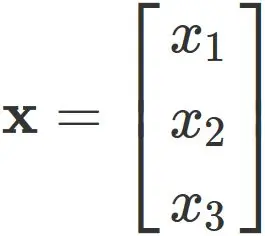
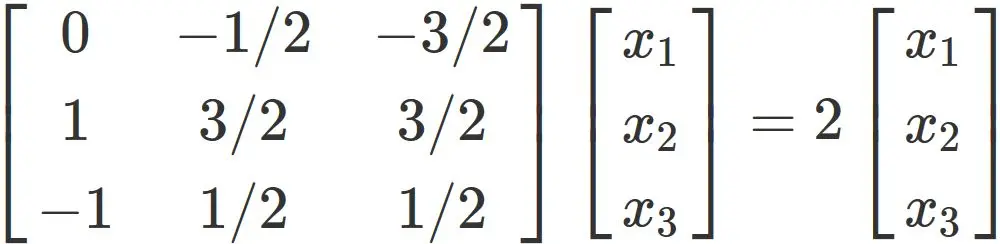
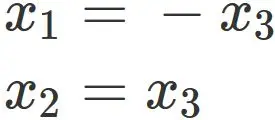
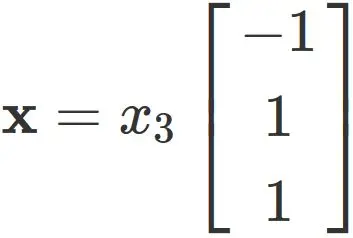
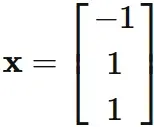
By (2.4), (2.5) and (2.6), we obtain the invertible matrix $P$ as
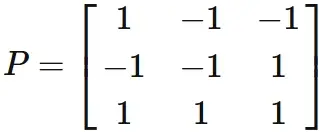
● Check the answer
We will check
whether the matrix $P$ in equation $(2.7)$
actually diagonalizes the matrix $A$,
that is, whether $P$, $A$ and $\Lambda$ satisfy
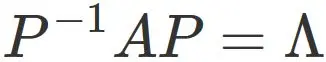
Derivation of $P^{-1}$
We will derive the inverse matrix $P^{−1}$ by Gaussian elimination. We define a matrix in which $P$ and the identity matrix $I$ are arranged side by side,
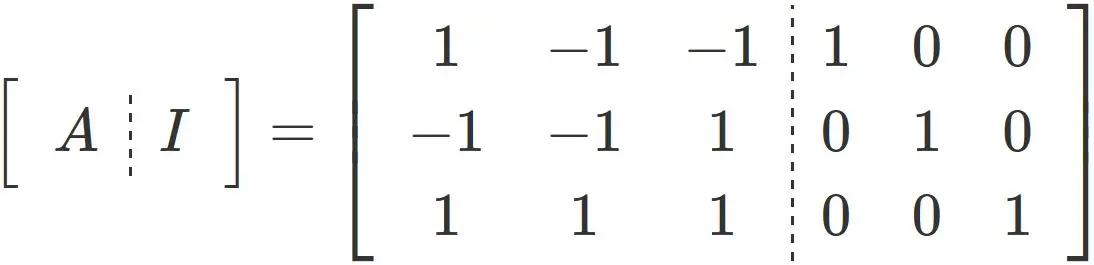


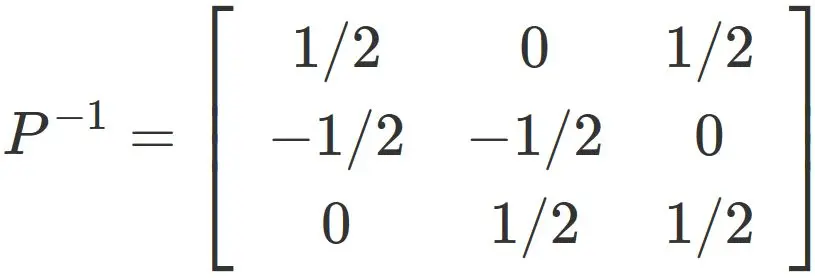
Check diagonalization
Now we can check the diagonalization as follows.