Computing square root : an example of Newton's method
Using Newton's method, When calculating the approximate value of $\sqrt{3}$,
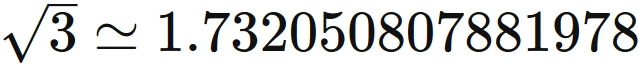
This value coincides with the correct value up to 10 digits. A specific calculation method will be described below. .
Explanation
Preparation:
The Newton's method is a method of obtaining a solution of the equation
$ f(x) = 0 $
by iterative calculations,
and the calculation of each step is defined by the following recurrence formula.
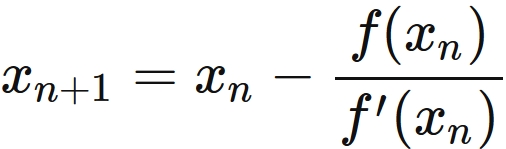
Using this method, it is known that correct numerical solutions can be obtained for some problems, and the problem of finding the square root is a typical example. In the following, we compute an approximated value of $ \sqrt {3} $ by Newton's method, and compare it with the correct value.
Computation:
Since $\sqrt{3}$ is one of the solutions of
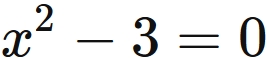
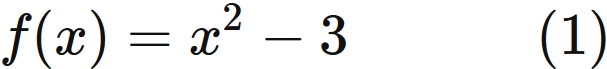
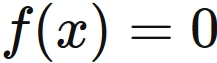
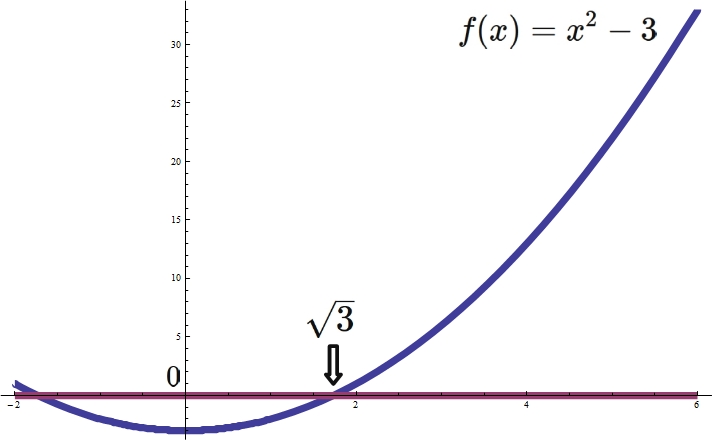

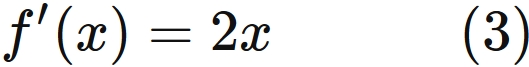

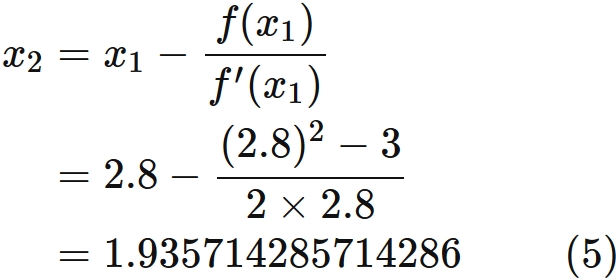
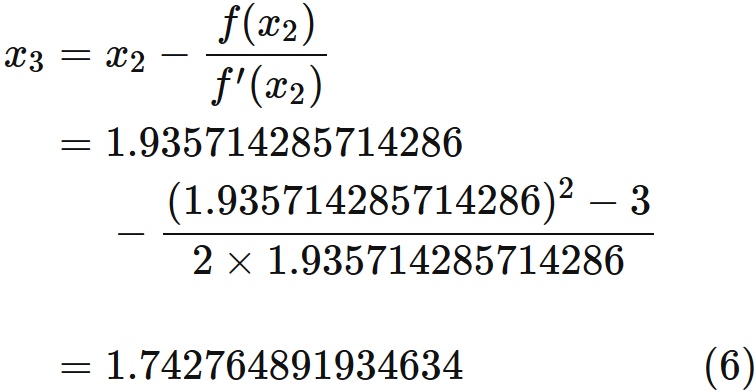
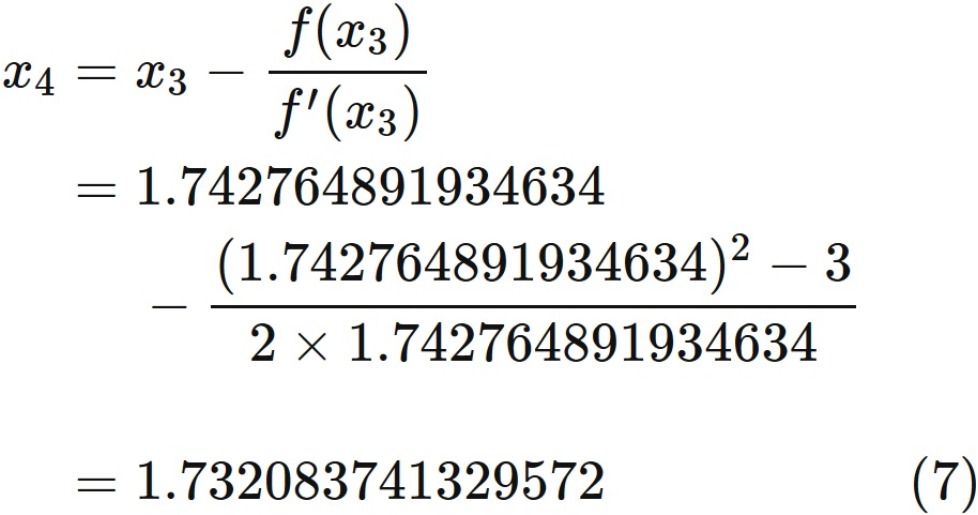
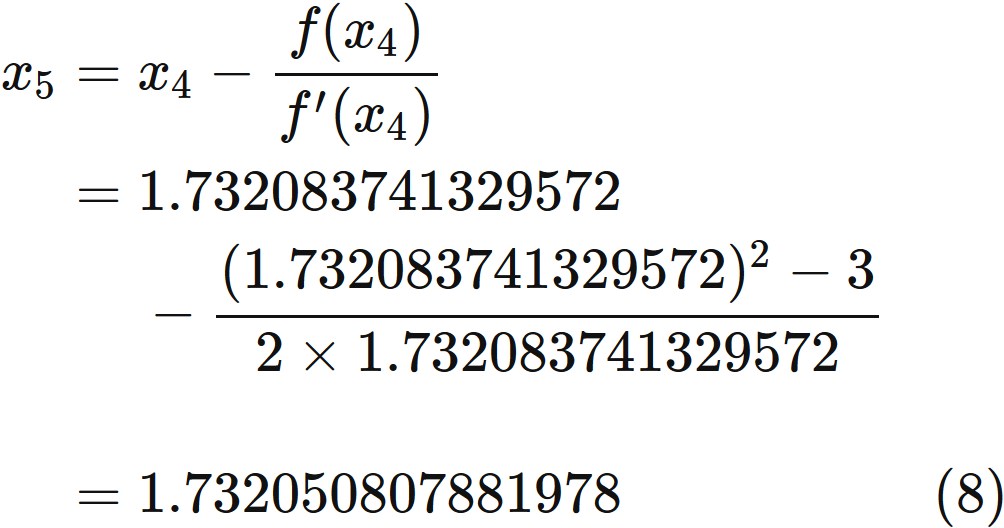
Since the correct value is
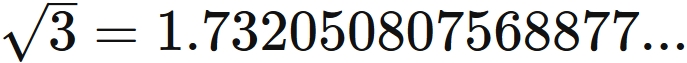
If we repeat the calculation like this, we can continue computing as much as we want. However, we need to halt the computation at some step. One strategy to stop at a certain iteration is to stop the computation when the absolute value of the change amount between each step becomes smaller than a predetermined value (threshold).
For example, the absolute value of the difference between $ x_ {5} $ and $ x_ {4} $ is less than $ 10 ^ {- 4} $ as follows
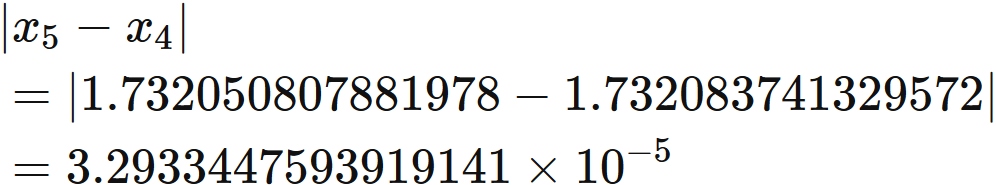
Caluculator of square root:
Enter the original value $ x $ and initial value $ x_ {0} $ in the following input form
and press the "Execute" button.
The result of the Newton's method for computing the square root of $ x $
is displayed up to the value of the fifth step.
Computation result
| $x_{1} = $ | |
| $x_{2} = $ | |
| $x_{3} = $ | |
| $x_{4} = $ | |
| $x_{5} = $ |
On convergence of calculation
In general,
the correct solution can not always be obtained by the Newton's method.
In addition,
the computation result may not converge.
However,
it is known that, under some conditions,
it converges to the correct solution.
One of the conditions is as follows.
The first and second derivative of the function both exist ($f(x) \in C^{2}$), and $f(x)$ satisfies
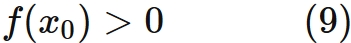

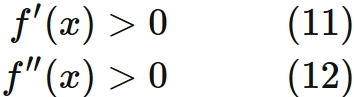
Here, let us make sure that Newton's method for obtaining the value of $ \sqrt {3} $ satisfies these conditions. If $x_{0}=5$, from $(1)$, we have
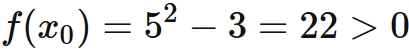
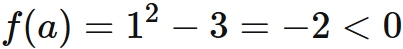
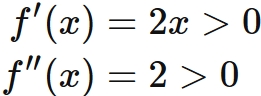
This guarantees that the computation result given by the above method always converge and the convergence value is $ \sqrt {3} $.