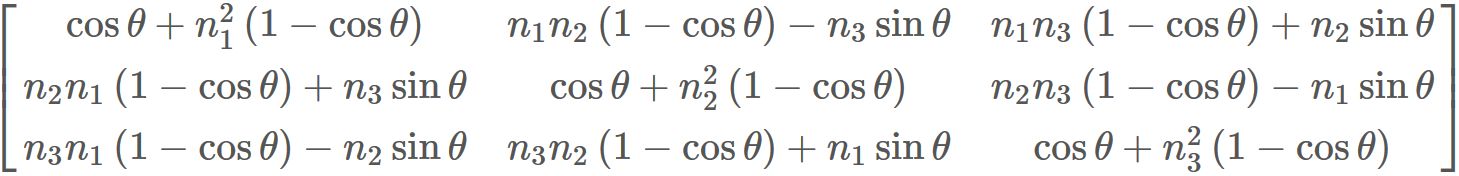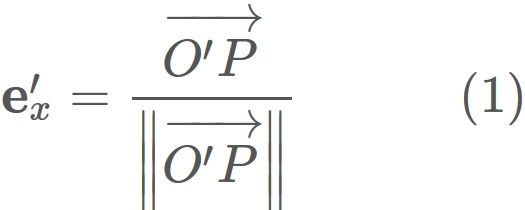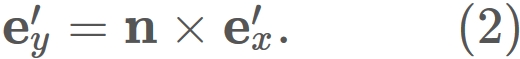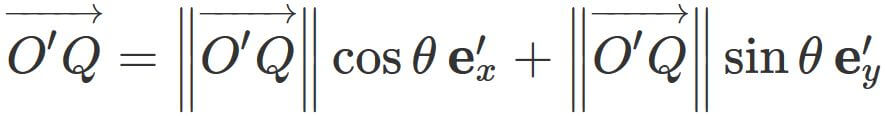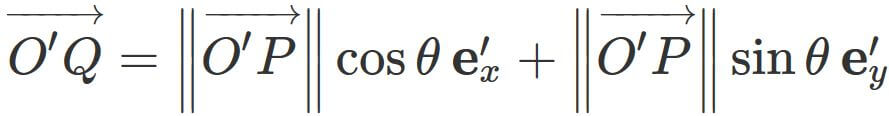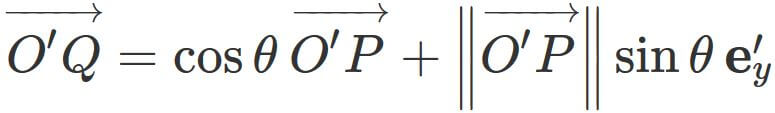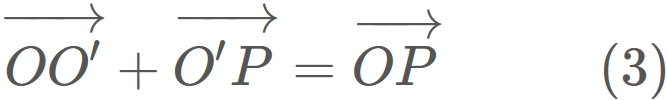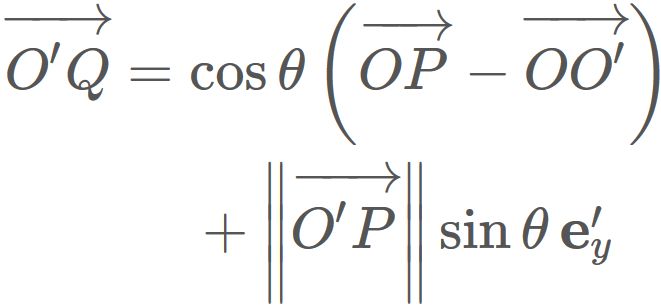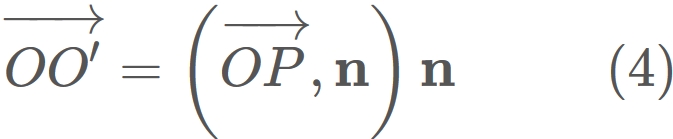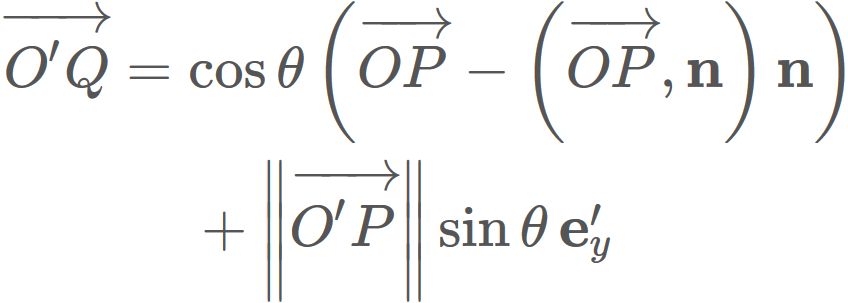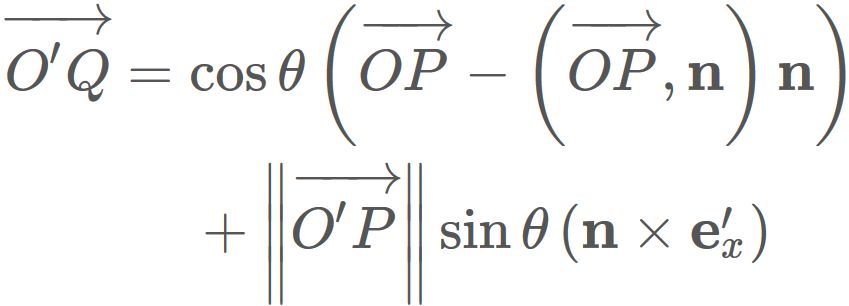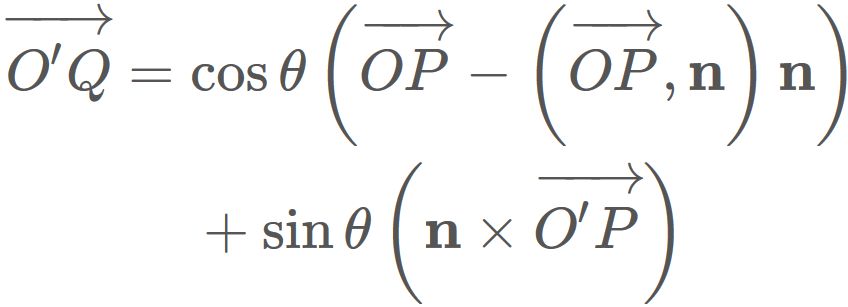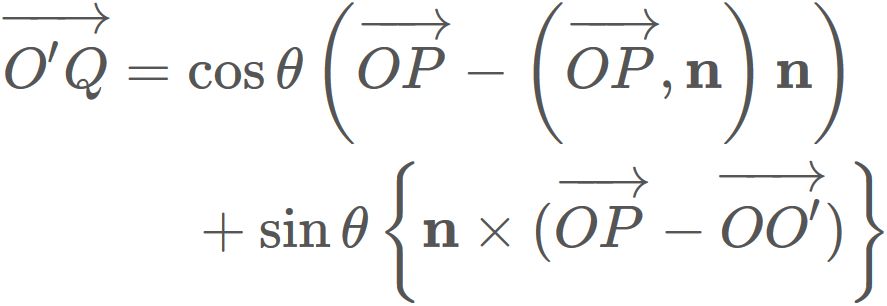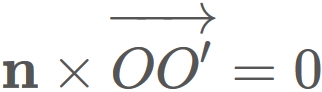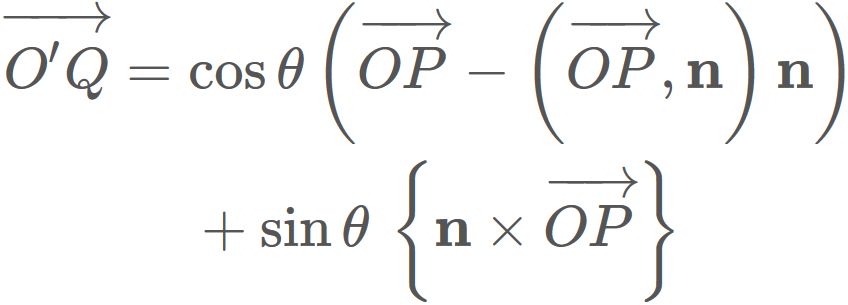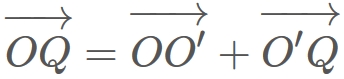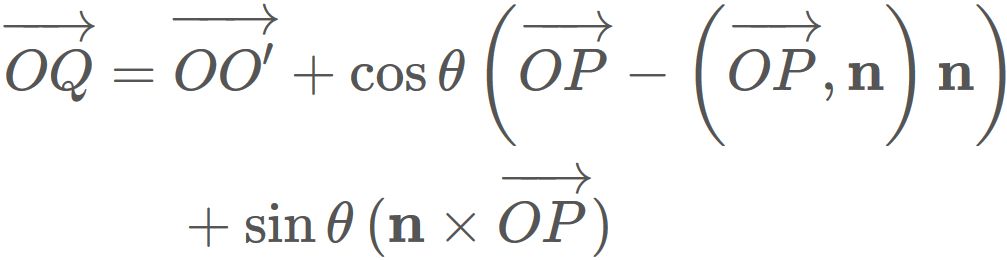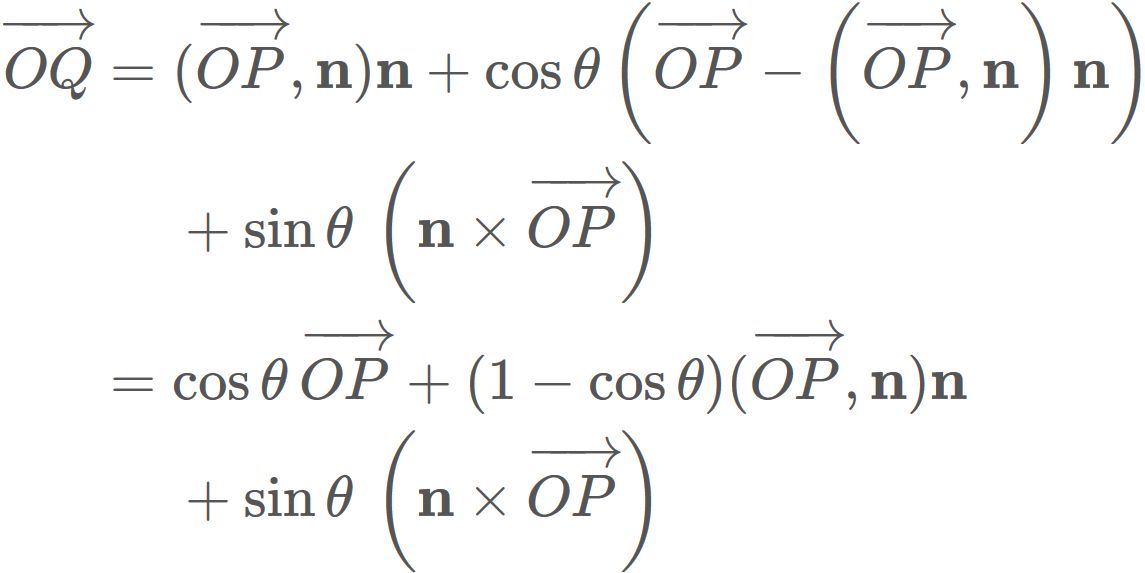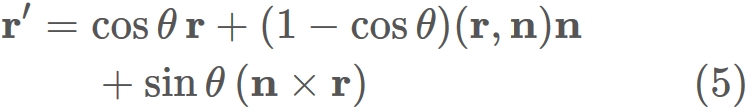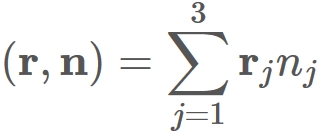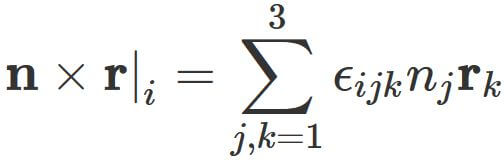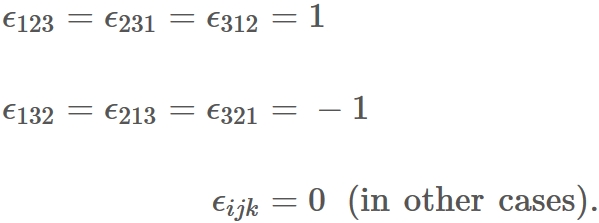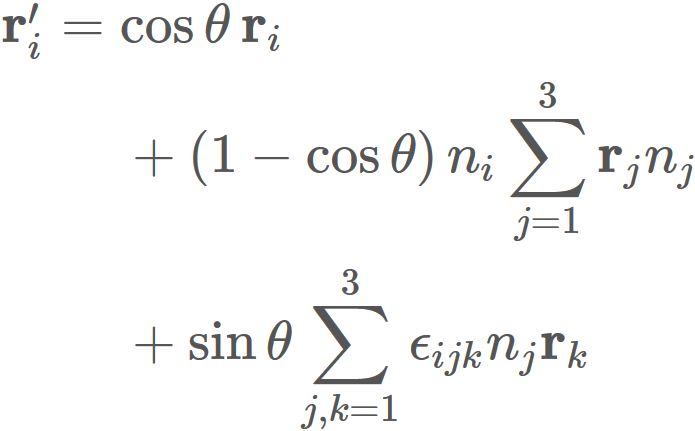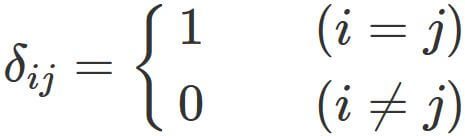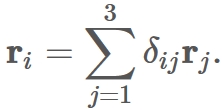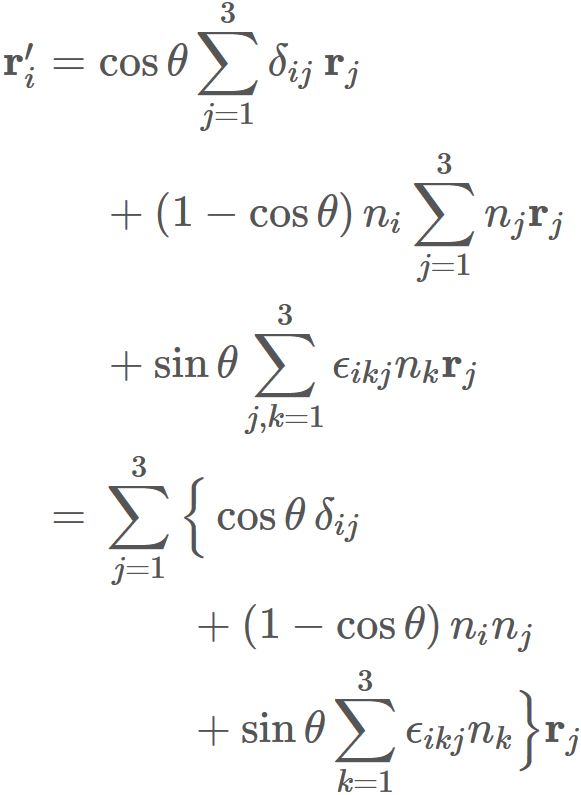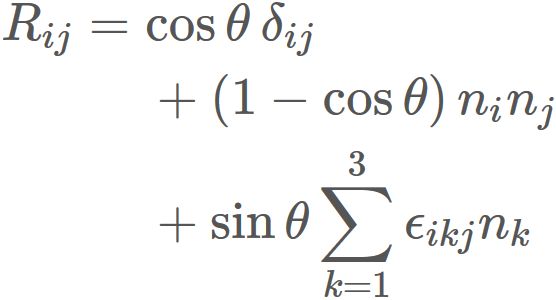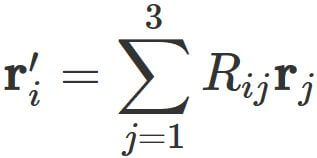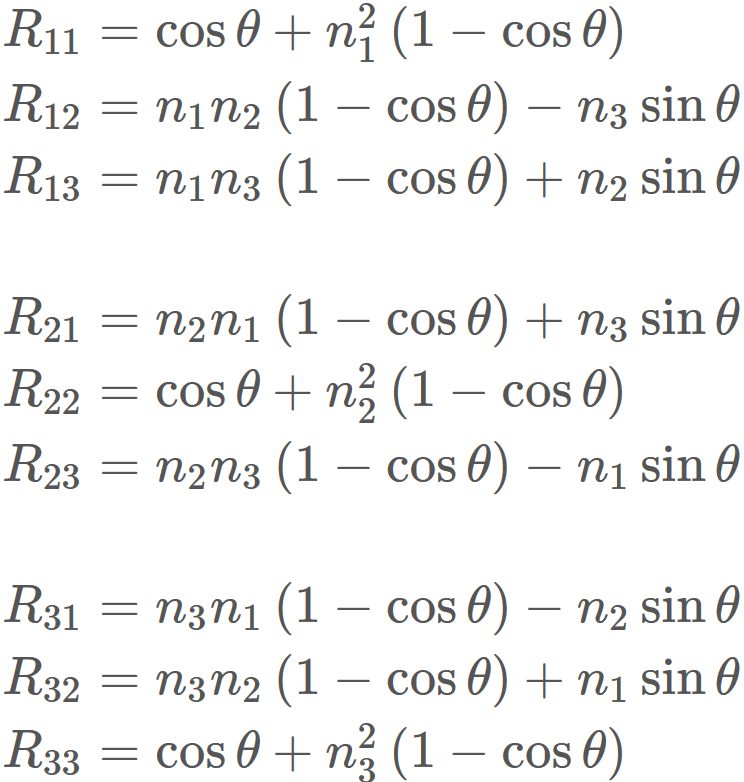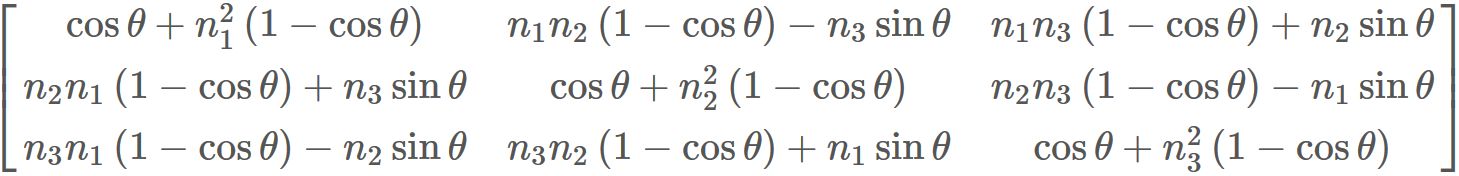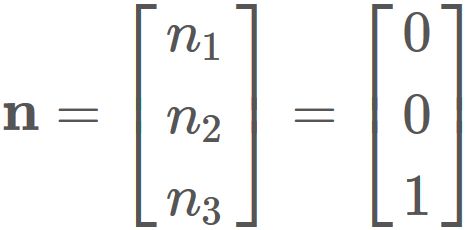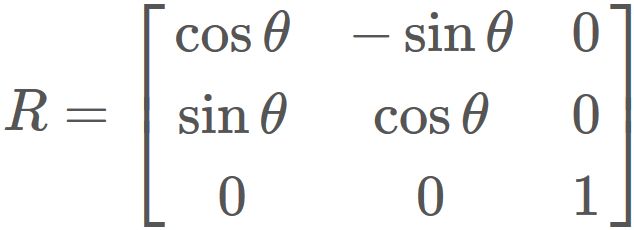Rodrigues' rotation formula

  Rotation about an arbitrary axis is represented by a rotation matrix , where $\mathbf{n} = [n_1, n_2, n_3]$ is an arbitrary axis of rotation and $\theta$ is a rotation angle
  This representation is called Rodrigues' rotation formula.

  Proof

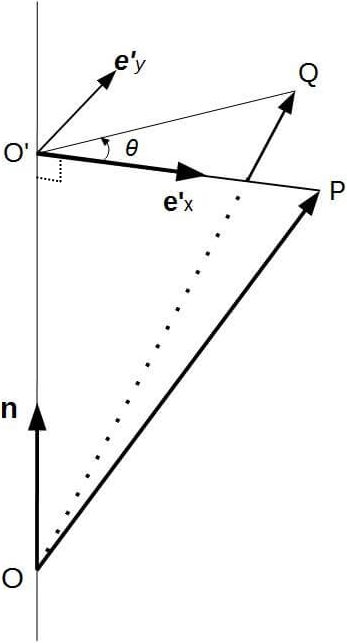
    Let $C$ be a coodinate system whose origin is $O$, $P$ be an arbitray position, $Q$ be the position obtained by rotating $P$ around an arbitrary axis $\mathbf{n}$ by a rotation angle $\theta$, and $O'$ be the projected position of $P$ onto $\mathbf{n}$. (See figure below.)   Let $\mathbf{e}'_{x}$ be a unit vector parallel to $\overrightarrow{O'P}$, and $\mathbf{e}'_{y}$ be a vector orthogonal to $\mathbf{e}'_{x}$ and $\mathbf{n}$. $\{ \mathbf{e}'_{x}, \mathbf{e}'_{y}, \mathbf{n} \}$ is an orthonormal basis of the three dimensinonal space.
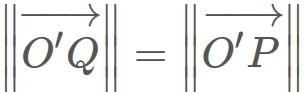
  Since $\theta$ is the rotation angle between $ \overrightarrow{O'Q}$ and $\mathbf{e}'_{x}$ , $\overrightarrow{O'Q} $ can be represended as The length of $\overrightarrow{O'Q}$ is equal to that of $\overrightarrow{O'P}$, i.e., , because $\overrightarrow{O'Q}$ is obtained by rotaion of $\overrightarrow{O'P}$ around $\mathbf{n}$. Therefore, we have   By substituing $(1)$ into this equation, we have As , $\overrightarrow{O'Q} $ can be written as As stated above, $O'$ is a projection of $P$ onto $\mathbf{n}$, i.e., Therefore we have By substituing $(2)$ into this equation, we have By substituing $(1)$ into this equation, we have Substituing $(4)$ into this equation, we have Here because $\mathbf{n}$ is parallel to $\overrightarrow{OO'} $. Therefore we have As , we have   Substituing $(4)$ into this equation, we have If we rewrite $\overrightarrow{OP}$ as $\mathbf{r}$ and $\overrightarrow{OQ}$ as $\mathbf{r}'$, this equation is expressed as This expression is called Rodrigues' rotation formula. We will derive its matrix representation below.
  We express the inner product in the second term of $(5)$ as and $i$-th element of the cross product in the third term as , where $\epsilon_{ijk}$ is Levi-Civita symboll defined as The $i$-th element of the expression $(4)$ can be written as Here, using Kronecker delta , $ \mathbf{r}_{i}$ can be written as Therefore we have By defining a matrix $R$ as , we see that $ \mathbf{r}'$ is obtained by operating $R$ on vector $ \mathbf{r}$, i.e.,   Specifically, each element of R is , and representing in the form of matrix, This is the matrix version of Rodrigues' rotation formula, which is used to represent a rotated position by a position before rotation.   If the rotation axis is the thrid axis, i.e., the rotation matrix, by using the above formula, is