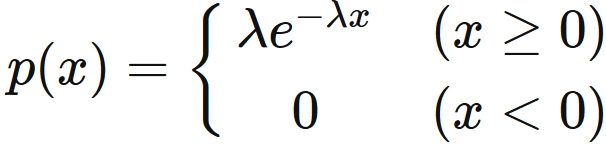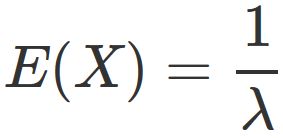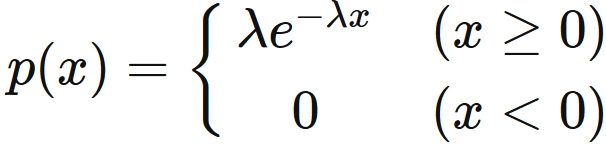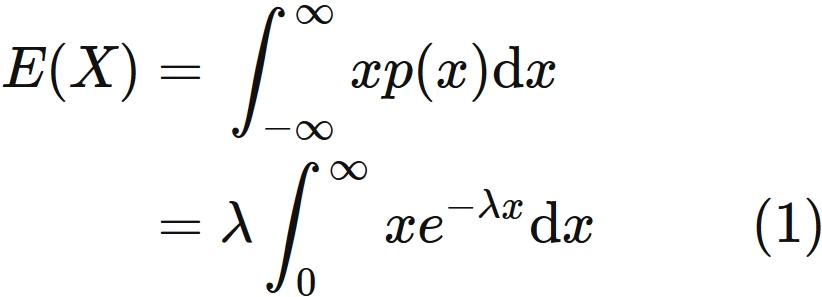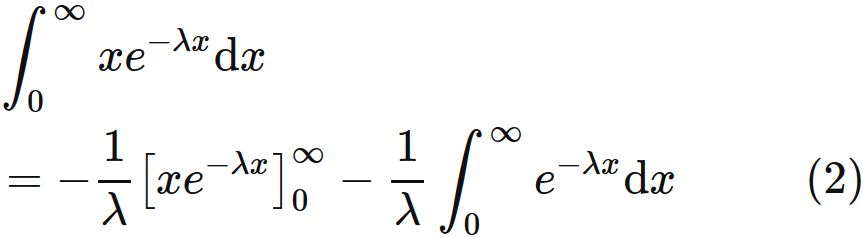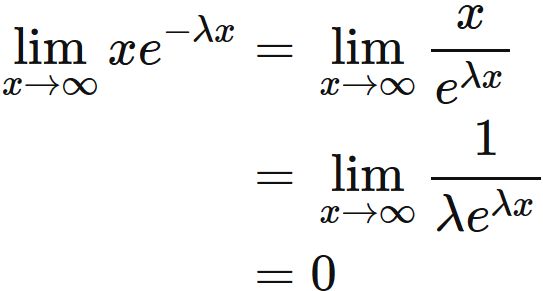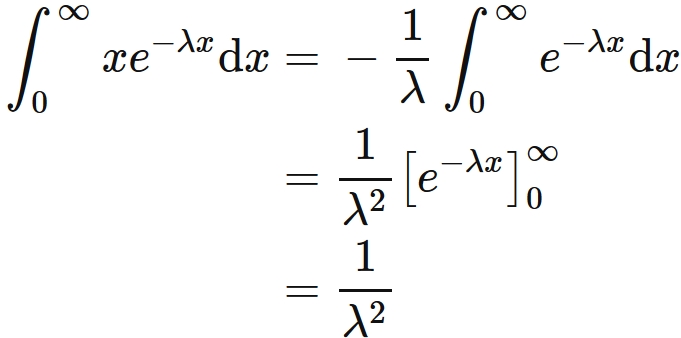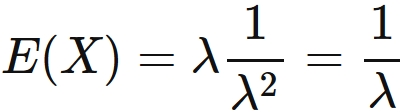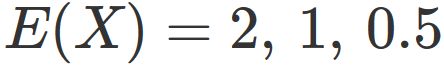The expectation value of the exponential distribution
The probability density function of the exponential distribution is
.
The expectation value for this distribution is
.
Proof
The probability density function of the exponential distribution is
.
By definition, the expectation value is
.
By partial integration,
the integral of the right-hand side is
.
The first term of the right-hand side of $(2)$ is zero, because
,
where we used L'Hospital's rule.
Therefore
the integral of $(2)$ is
.
Substituting this into $(1)$,
we obtain
.
Example
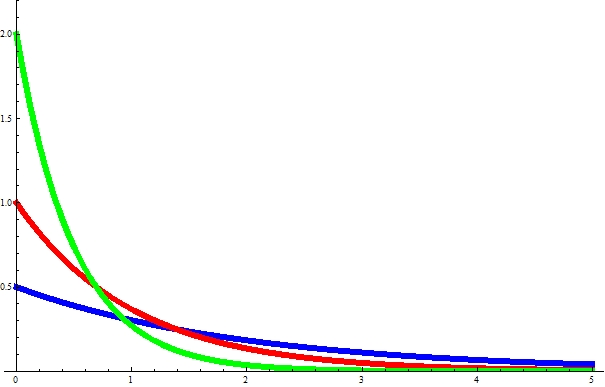
The figure below is the exponential distribution for $ \lambda = 0.5 $ (blue),
$ \lambda = 1.0 $ (red), and $ \lambda = 2.0 $ (green).
As the value of $ \lambda $ increases,
the distribution value closer to $ 0 $ becomes larger,
so the expected value can be expected to be smaller.
In fact, the expected value for each $ \lambda $ is
.
The larger the value of $ \lambda $ is, the smaller the expectation value is.