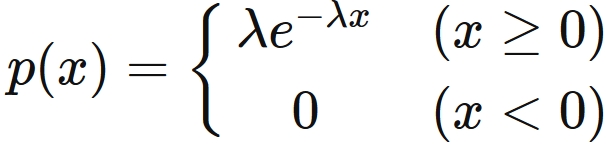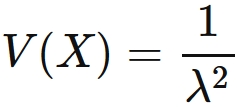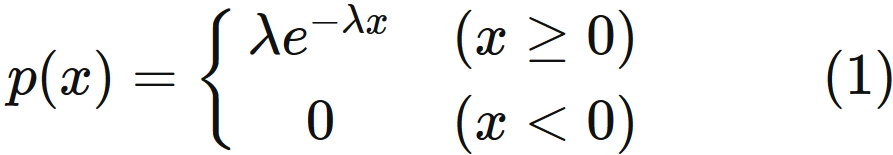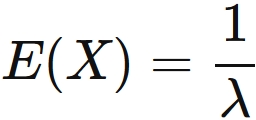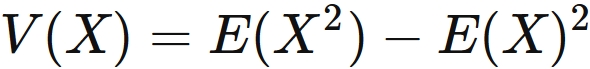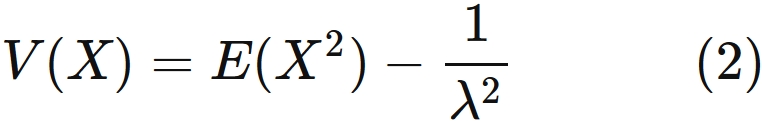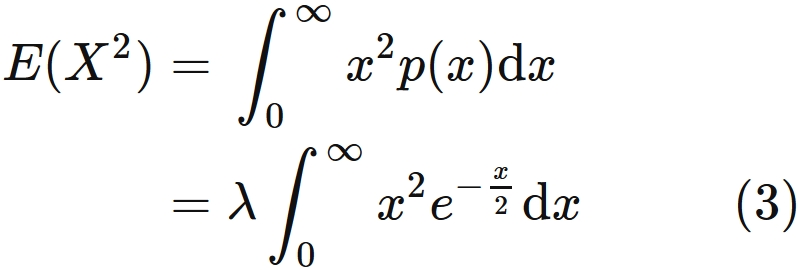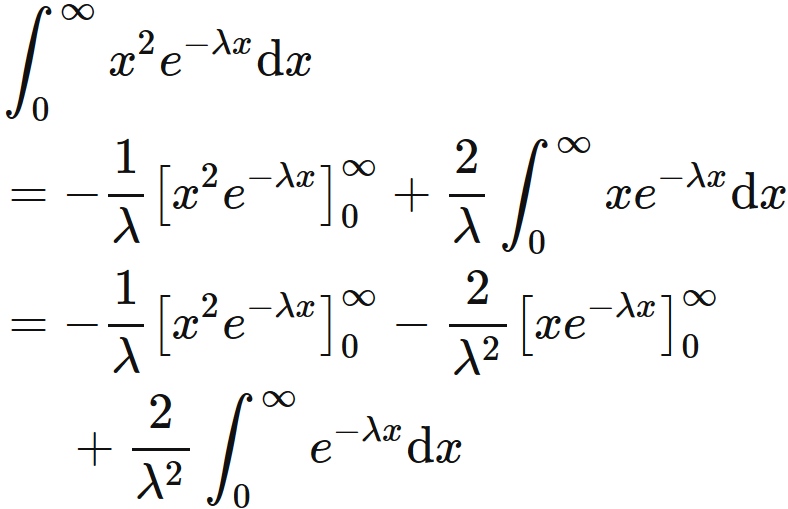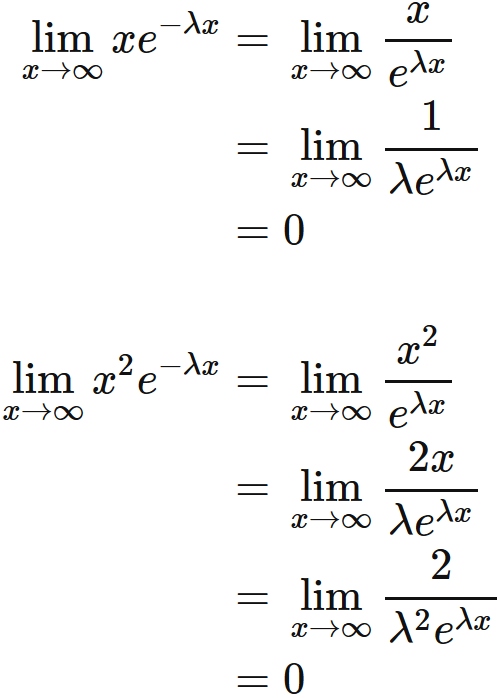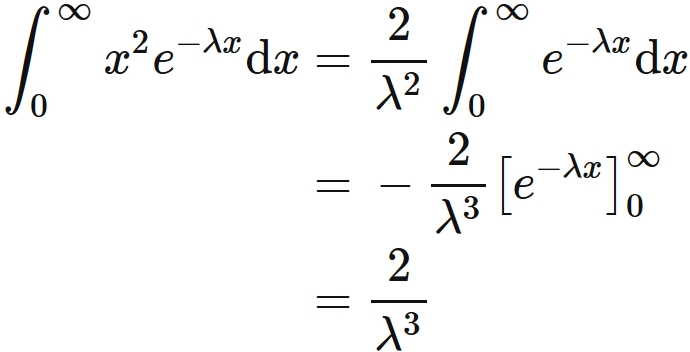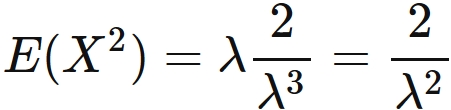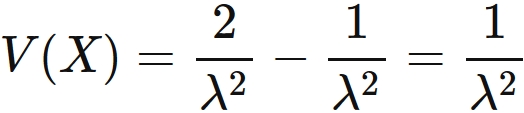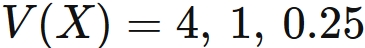The variance of the exponential distribution

  The probability density function of the exponential distribution is . The variance for this distribution is .

Proof

  The probability density function of the exponential distribution is . The expectation value for this distribution is . (See The expectation value of the exponential distribution.)
  In general, the variance is equal to the difference between the expectation value of the square and the square of the expectation value, i.e., Therefore we have If the expectation value of the square is found, the variance is obtained.
  The expectation value of the square is , where we used $(1)$.
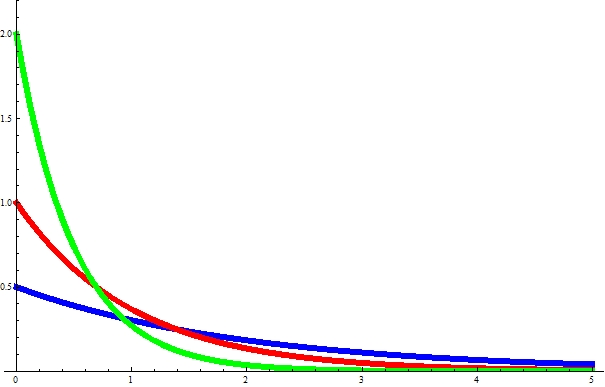
  By partial integration, the integral of the right-hand side is . Here, we see that the first and the second terms of the right-hand side of this equation are zero, because , where we used L'Hospital's rule. Therefore, we have Substituting this equation to $(2)$, we obtain .   The figure below is the exponential distribution for $ \lambda = 0.5 $ (blue), $ \lambda = 1.0 $ (red), and $ \lambda = 2.0$ (green). We see that the smaller the $\lambda$ is, the more spread the distribution is. In fact, the variance for each $\lambda$ is The larger $\lambda$ is, the smaller the variance is.