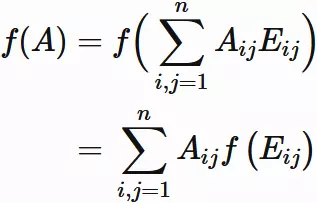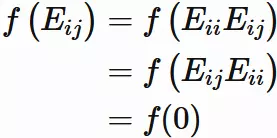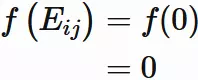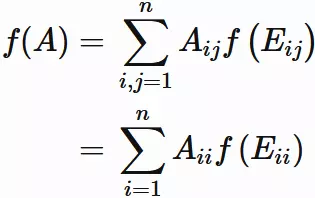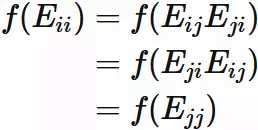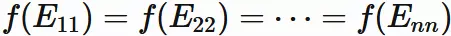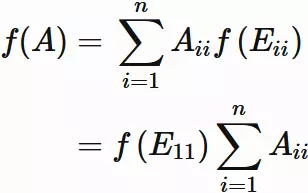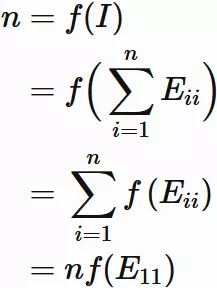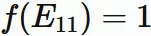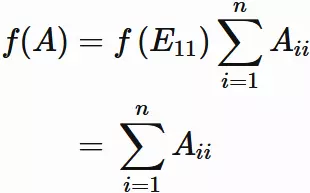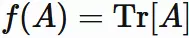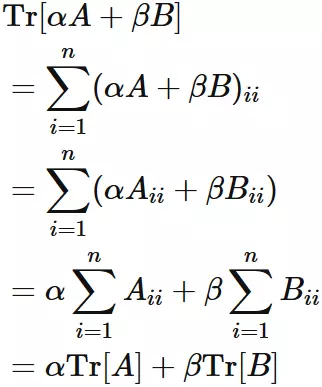Trace - properties and formulas -
| Definition | |
|---|---|
| - | Definition |
| - | Examples |
| Properties | |
|---|---|
| - | Symmetry |
| - | Cyclic property |
| - | Linearity |
| - | Defined by three properties |
Definition
The trace of an $n \times n$ square matrix $A$ is the sum of the diagonal components of the matrix,
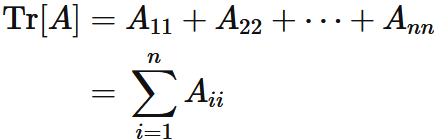
Examples
Let $A$ be a squared matrix defined as
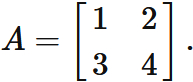
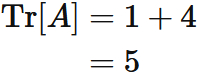
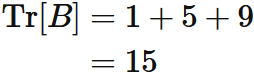
Symmetry
The trace of the product of two matrices is equal to the trace of the product in which order is swapped.
Let $A$ and $B$ be an $m \times n$ and an
$n \times m$ matrix, respectively,
then
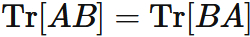
Proof
$AB$ is an $m \times m$ matrix. By the definition of trace, the trace of $AB$ is
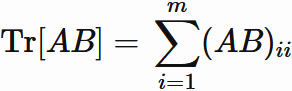 Using the rule of matrix product,
we have
Using the rule of matrix product,
we have
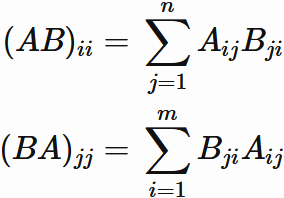 then
then
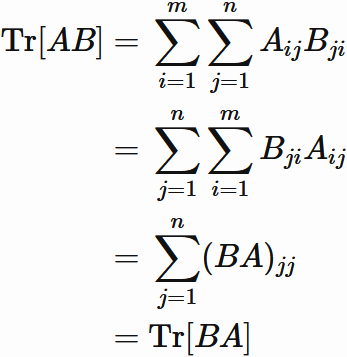
$AB$ is an $m \times m$ matrix. By the definition of trace, the trace of $AB$ is
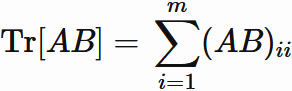
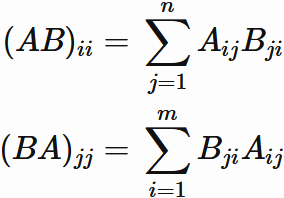
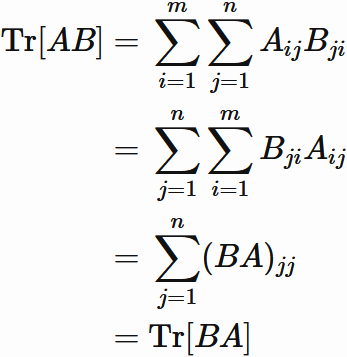
Cyclic property
Let $A$, $B$, $C$
be
$m\times n$,
$n \times l$,
$l \times m$
matrix, respectively.
The trace of the product of three matrices is invariant even if the order of the products is cyclically changed:
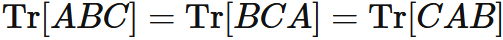
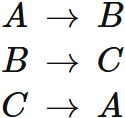
Proof
We use the symmetry of the trace. Using the symmetry of $A$ and $BC$, we have
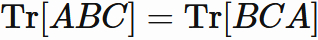 Using the symmetry of
$AB$
and
$C$,
we have
Using the symmetry of
$AB$
and
$C$,
we have
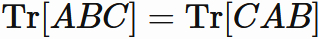 Therefore,
Therefore,
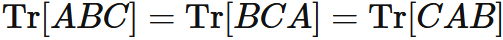
We use the symmetry of the trace. Using the symmetry of $A$ and $BC$, we have
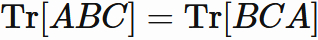
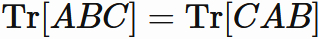
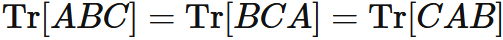
Linearity
Let $A$ and $B$ be square matrices and
$\alpha$ and $\beta$ be scalars.
The trace is linear:
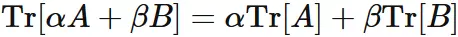
Defined by three properties
Let $A$ and $B$ are $n \times n$ matrices,
$\alpha$ and $\beta$ be scalars,
and $f$ be a function of $n \times n$ matrix.
If the function $f$ satisfies
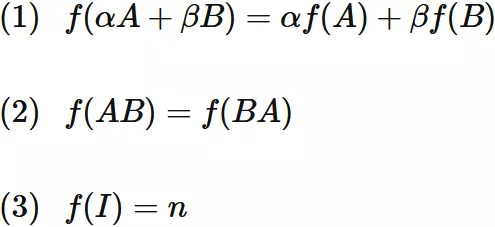
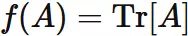
Proof
 If
$i \neq j$,
The following equations holds.
If
$i \neq j$,
The following equations holds.
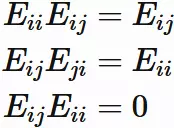 $$
\tag{6.1}
$$
An arbitrary $n \times n$ matrix $A$
can be written by $E_{ij}$ as
$$
\tag{6.1}
$$
An arbitrary $n \times n$ matrix $A$
can be written by $E_{ij}$ as
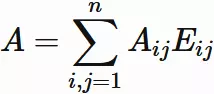 $$
\tag{6.2}
$$
, where $A_{ij}$ is $i$-th row and $j$-th column element of $A$.
For the identity matrix $I$,
we have
$$
\tag{6.2}
$$
, where $A_{ij}$ is $i$-th row and $j$-th column element of $A$.
For the identity matrix $I$,
we have
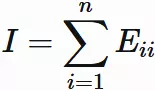
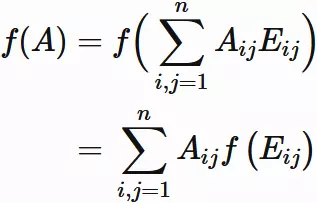 $$
\tag{6.3}
$$
For
$i \neq j$,
Prop.$(2)$ and
Eq.$(6.1)$ give
$$
\tag{6.3}
$$
For
$i \neq j$,
Prop.$(2)$ and
Eq.$(6.1)$ give
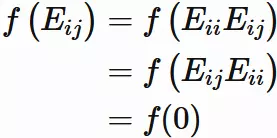 Here,
considering the case of
$\alpha = \beta = 0$ in Prop.$(1)$,
$
f(0) = 0
$
.
We have
Here,
considering the case of
$\alpha = \beta = 0$ in Prop.$(1)$,
$
f(0) = 0
$
.
We have
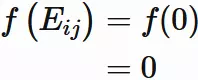 Using this equation,
Eq.$(6.3)$ can be written as
Using this equation,
Eq.$(6.3)$ can be written as
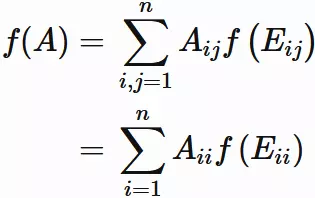 $$
\tag{6.4}
$$
Here,
we see from Eq.$(6.1)$ and Prop.$(2)$ that
$$
\tag{6.4}
$$
Here,
we see from Eq.$(6.1)$ and Prop.$(2)$ that
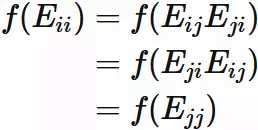 that is,
that is,
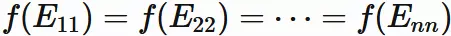 $$
\tag{6.5}
$$
From this,
Eq.$(6.4)$ can be rewritten as
$$
\tag{6.5}
$$
From this,
Eq.$(6.4)$ can be rewritten as
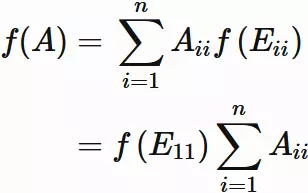 $$
\tag{6.6}
$$
Note from
Props.$(1)$, $(3)$ and Eq.$(6.5)$ that
$$
\tag{6.6}
$$
Note from
Props.$(1)$, $(3)$ and Eq.$(6.5)$ that
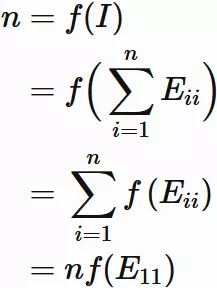 , we have
, we have
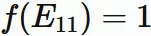 Eq.(6.6) can be rewritten as
Eq.(6.6) can be rewritten as
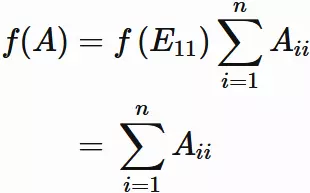 The righthand side of this equation is the trace of $A$.
Therefore, we obtain
The righthand side of this equation is the trace of $A$.
Therefore, we obtain
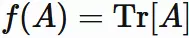
Matrix $E_{ij}$
Let $E_ {ij}$
be $n \times n$ matrix with only the
$i$-th row and
$j$-th column element being $1$
and the other components being $0$.

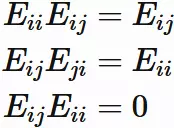
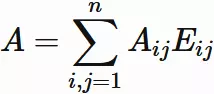
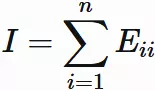
Proof
From
Prop.$(1)$
and
Eq.$(6.2)$,