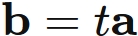Proof of Triangle Inequality and Equality Condition - SEMATH INFO -
For any real vectors $\mathbf{a}$ and $\mathbf{b}$,
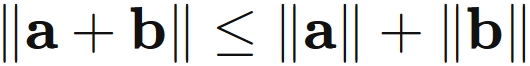
Proof
Geometrically, the triangular inequality is an inequality expressing that the sum of the lengths of two sides of a triangle is longer than the length of the other side as shown in the figure below.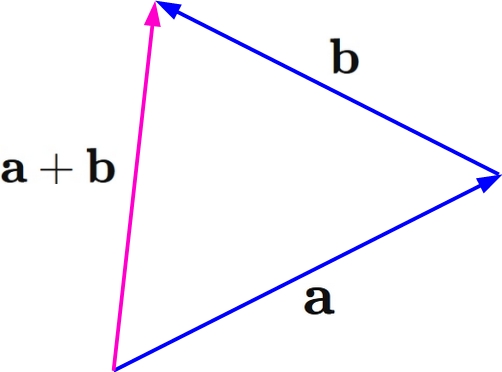
Let $\mathbf{a}$ and $\mathbf{b}$ be real vectors. The square of the norm of $\mathbf{a} + \mathbf{b}$ satisfies
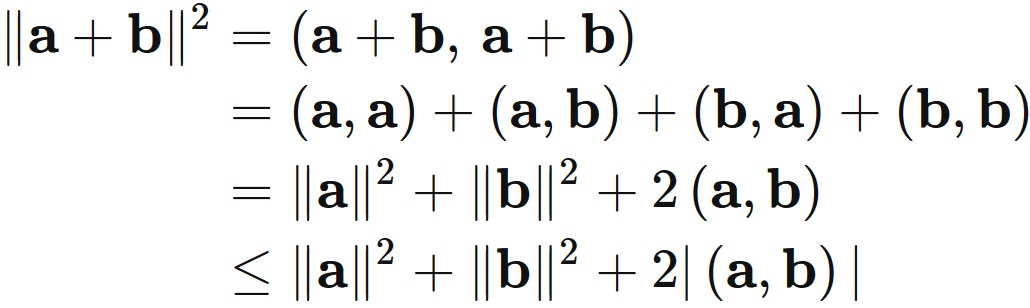
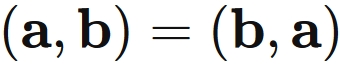
Applying the Schwarz inequality,
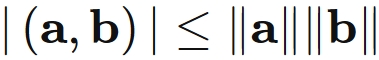
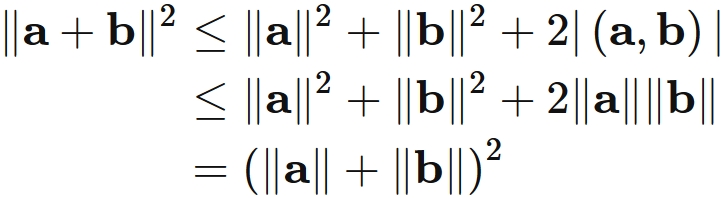
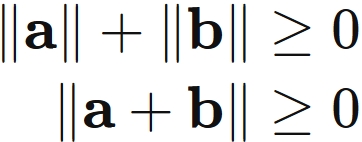
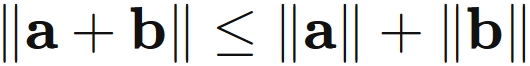
Equality Condition
We will discuss the equality condition of the triangular inequality.
First, one of the equality condition of the triangle inequality is $ \mathbf{a} = 0 $ or $ \mathbf{b} = 0 $ , because, in this case, it is clear that
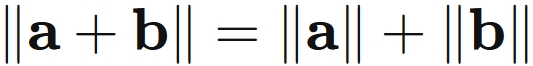
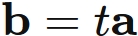
This can be understood by considering as follows. In the above proof of the triangle inequality, we only use relations that hold for all vectors other than the Schwarz inequality,
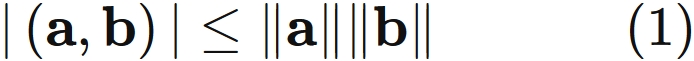
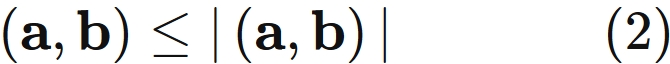
It is known that the equality condtion of Schwarz inequality $(1)$ is that $\mathbf{a}$ and $\mathbf{b}$ are parallel,
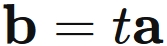
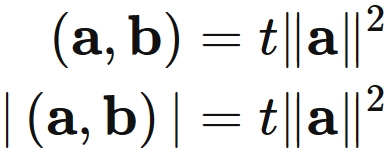
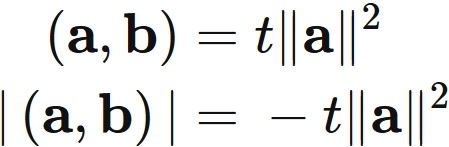
We thus see that the equality condtion of $(1)$ and $(2)$ is that