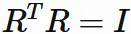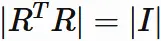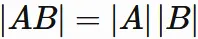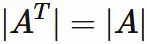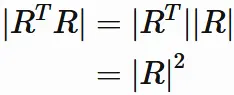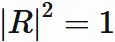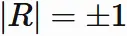Orthogonal matrix - properties and formulas -
| Table of contents | |
|---|---|
| - | Definition |
| - | Example |
| - | Product |
| - | Inverse |
| - | Determinant |
Definition
Let $R$ be a square matrix.
$R$ is called orthtonal matrix
if it satisfies
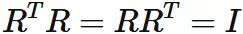
Example
Show that the following matrix
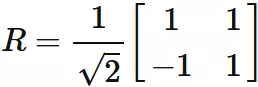
Explanation
By calculating concretely, we have
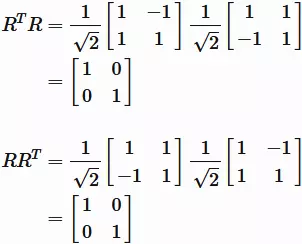Therefore, $R$ is an orthogonal matrix.
By calculating concretely, we have
Product
If $R$ and $S$ are orthogonal matrices,
then the product $RS$ are an orthogonal matrix as well.
It satisfies
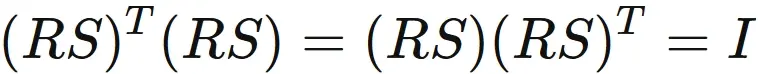
Proof
Let $R$ and $S$ are orthogonal matrices. They satisfy
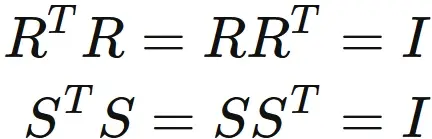where $I$ is the identity matrix.
By the property of
product of transopsed matrix
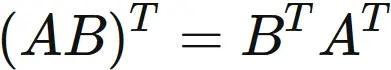We see that
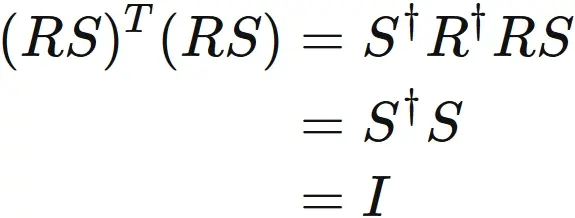and
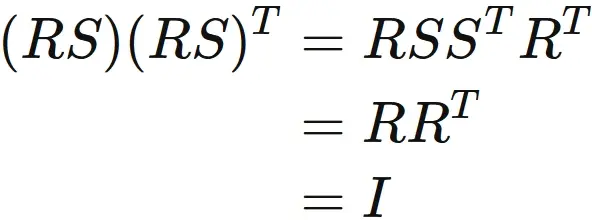Therefore we obtain
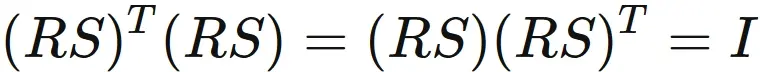The product $RS$ are an orthogonal matrix as well.
Let $R$ and $S$ are orthogonal matrices. They satisfy
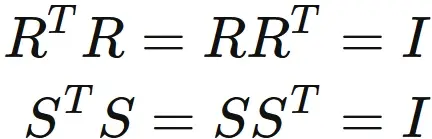
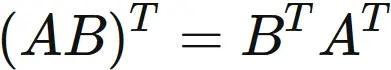
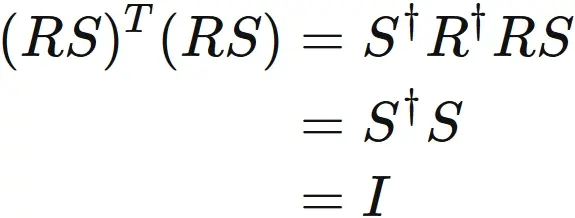
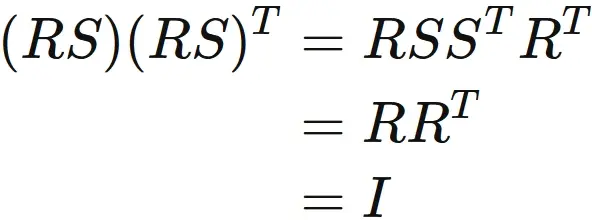
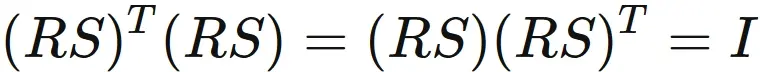
Inverse
The inverse matrix of an orthogonal matrix R is the transpose of $R$,
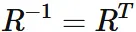
Proof
In general, the inverse matrix of a square matrix $A$ is a matrix $B$ that satisfies
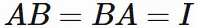, where $I$ is the identity matrix.
Such $B$ is expressed as
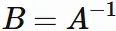With this in mind,
looking at the definition of an orthogonal matrix,
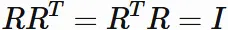we see that $R^{T}$ is the inverse of $R$.
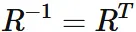
In general, the inverse matrix of a square matrix $A$ is a matrix $B$ that satisfies
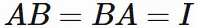
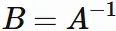
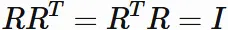
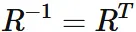
Determinant
The determinant of an orthogonal matrix $R$ is $\pm 1$.
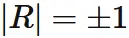
Proof
Let $R$ be an orthogonal matrix. We have
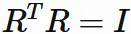The determinant is
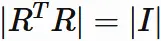$$
\tag{5.1}
$$
In the left-hand side,
the property of product of determinant
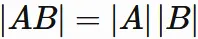and the property of determinant of transpose
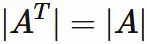give
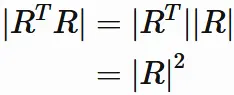In the right-hand side of $(5.1)$,
the determinant of identity matrix is $1$.
We have
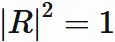Therefor we obtain
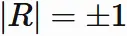
Let $R$ be an orthogonal matrix. We have