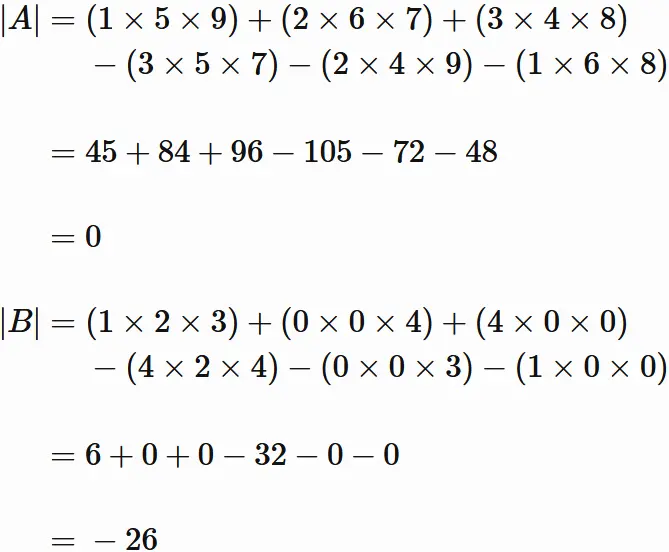Determinant of a 3x3 matrix
| 目次 | |
|---|---|
| - | $3\times 3$ determinant |
| - | Example |
| - | Calculator |
| - | Rule of Sarrus |
$3 \times 3$ determinant
Find the determinant of a 3x3 matrix,

Proof
The cofactor expansion of $A$ along the first column is
 Calculating the 2x2 determinant in each term,
Calculating the 2x2 determinant in each term,
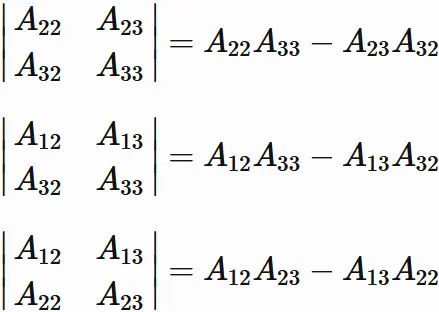 We obtain
We obtain
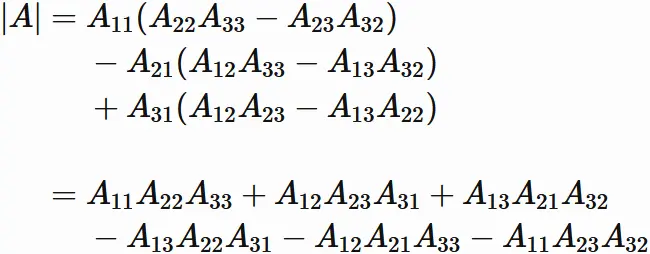
The cofactor expansion of $A$ along the first column is

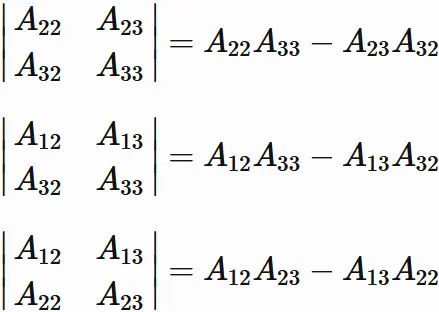
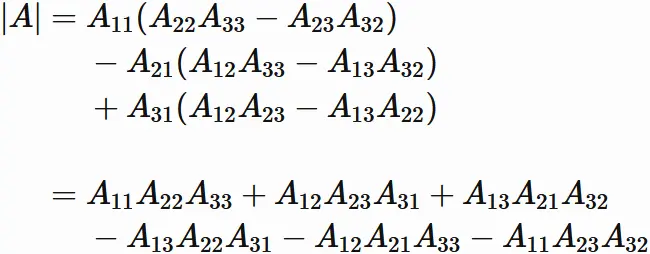
Examples
Find the determinants of the following matrices.
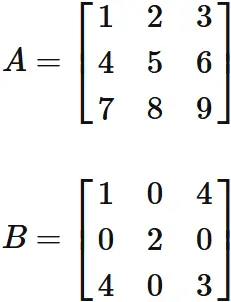
Calculator
Enter a 3x3 matrix and press "Execute" button. Then the determinant is displayed.
$|A|$
=
Rule of Sarrus
The $3 \times 3$ determinant is
a bit more complicated than the $2 \times 2$ determinant,
so there is a visual formula to remember.
Let us draw five lines from the top left to the bottom right of a $3 \times 3$ matrix.
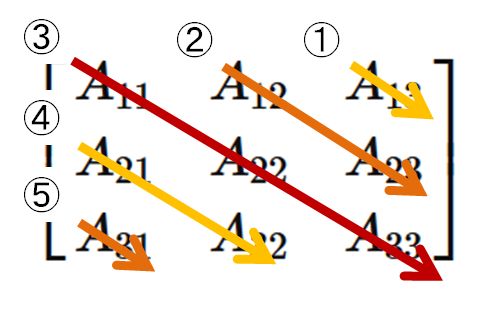
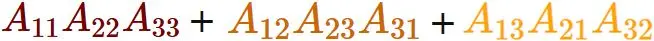
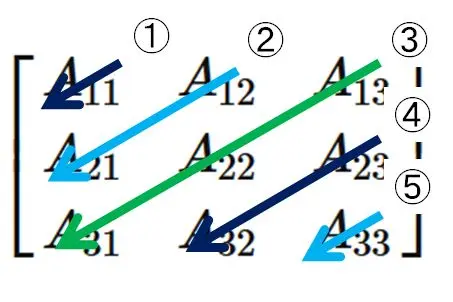

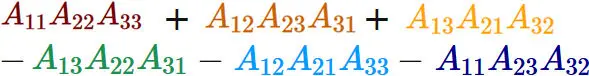
Thus, the determinant of a $3 \times 3$ matrix is obtained by adding the terms obtained by drawing lines from the upper left to the lower right, and subtracting the terms obtained by drawing lines from the upper right to the lower left. This visual formula is called Rule of Sarrus.