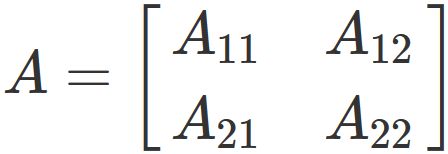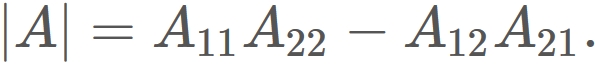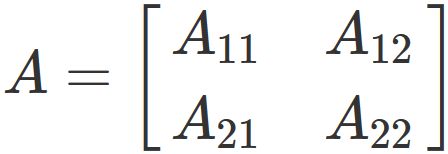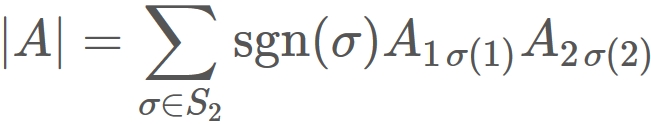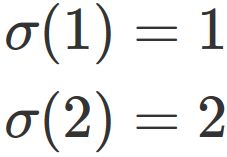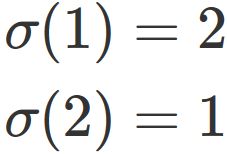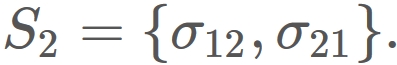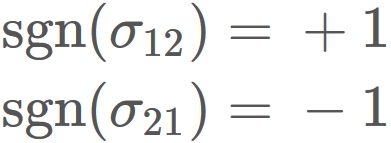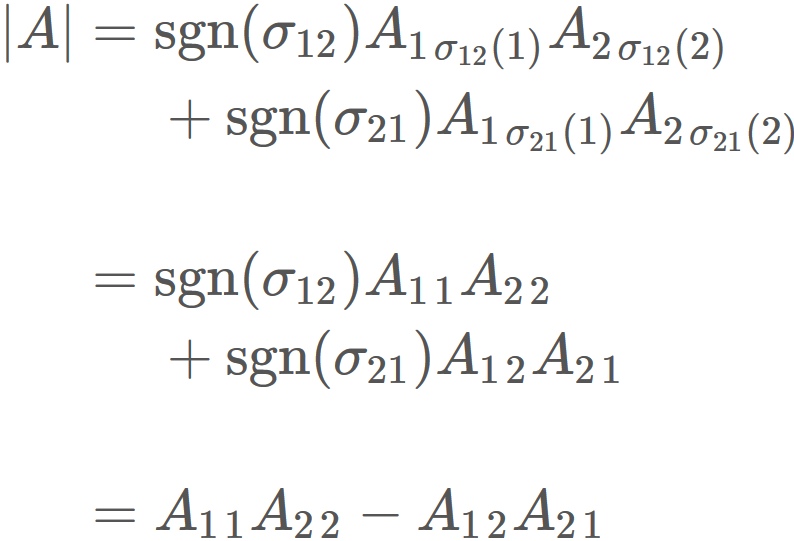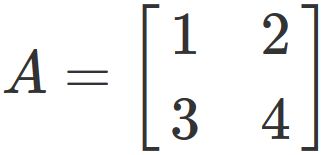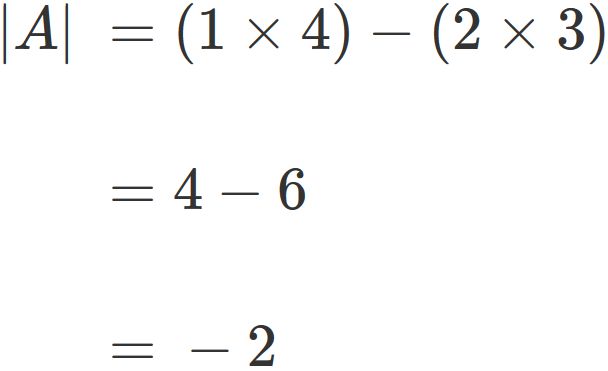Determinant 2x2

  Show the determinant of a 2x2 matrix is

  Proof

  By definition of determinant, the determinant of a 2x2 matrix is where $\sigma$ is a one-to-one mapping from a set $\{1,2 \}$ to the same set. There are two cases that and Let $\sigma_{12}$ be the above case and $\sigma_{21}$ be the below case. $S_{2}$ is a set having $\sigma_{12}$ and $\sigma_{21}$ as elements, $ \mathrm{sgn}(\sigma) $ is a sign assigned to $\sigma_{12}$ and $\sigma_{21}$ as ($\mathrm{sgn}(\sigma)$ becomes negative if the order of number $\{1,2\}$ is changed odd times.)
  Therefore $|A|$ is written as Using the above result, the determinant of a 2x2 matrix is   Enter a 2x2 matrix and press "Execute" button. Then its determinant is displayed.