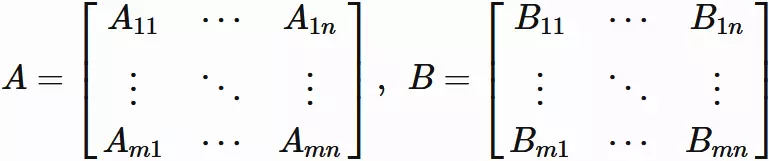Transpose - properties and formulas -
Definition
A matrix in which the row and column elements of a matrix are exchanged is called the transposed matrix of that matrix.
The transpose of a matrix $A$ is represented as $A^ {T}$.
The $i$-th row, j-th column element of $A^T$ is the $j$-th row, $i$-th column element of $A:$
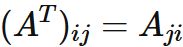
Explanation
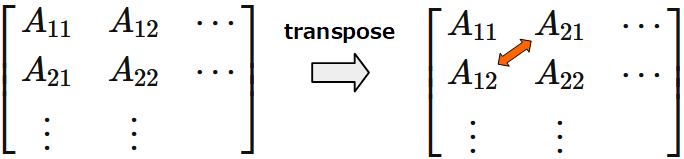
The $i$-th row, $j$-th column element of $A^T$ is the $j$-th row, $i$-th column element of $A$. For example, if $i=1$ and $j=2$,
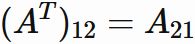 And if $i=2$ and $j=1$,
And if $i=2$ and $j=1$,
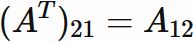 By transposition,
each element is exchanged corssing diagonal elements.
By transposition,
each element is exchanged corssing diagonal elements.
 Since $(A^{T})_{ii} = A_{ii}$,
each diagonal element is unchanged.
Since $(A^{T})_{ii} = A_{ii}$,
each diagonal element is unchanged.
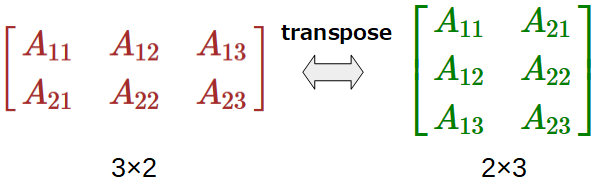
In general, the size of a traspose matrix is different from its original one. If $A$ is an $m \times n$ matrix, then $A^{T}$ is an $n \times m$ matrix.
 If $A$ is a square matrix,
the size of $A^{T}$ is the same as that of $A$.
If $A$ is a square matrix,
the size of $A^{T}$ is the same as that of $A$.
A column matrix has only one column but any number of rows. A row matrix has only one row but any number of columns. Transpose transforms a column matrix to a row matrix, and vice versa.
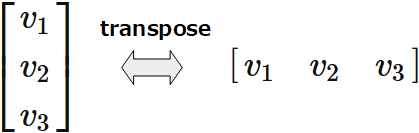 Various matrices are defined by transpose. For example,
Various matrices are defined by transpose. For example,
The $i$-th row, $j$-th column element of $A^T$ is the $j$-th row, $i$-th column element of $A$. For example, if $i=1$ and $j=2$,
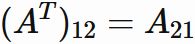
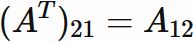

In general, the size of a traspose matrix is different from its original one. If $A$ is an $m \times n$ matrix, then $A^{T}$ is an $n \times m$ matrix.

A column matrix has only one column but any number of rows. A row matrix has only one row but any number of columns. Transpose transforms a column matrix to a row matrix, and vice versa.
- If $A^{T}=A$, $A$ is called a symmetric matrix.
- If $A^{T}A=AA^{T}=I$, $A$ is called an orthogonal matrix.
Examples
The transposed matrix of matrix
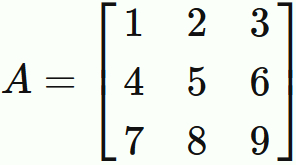
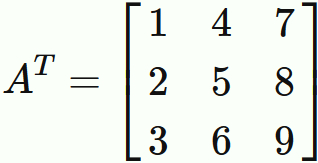
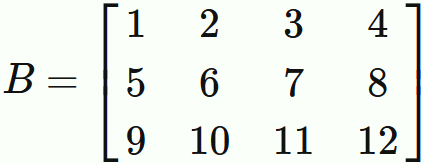
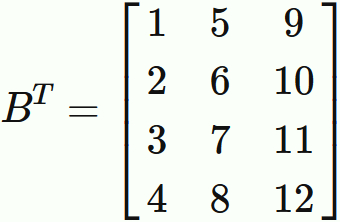
Product
The transposed matrix of the product of two matrices
is equal to the product of the transposed matrices in which the order of the products is reversed:
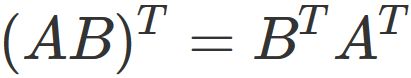
Proof
Let $A$ be a $l \times m$ matrix, and $B$ be a $m \times n$ matrix, written as
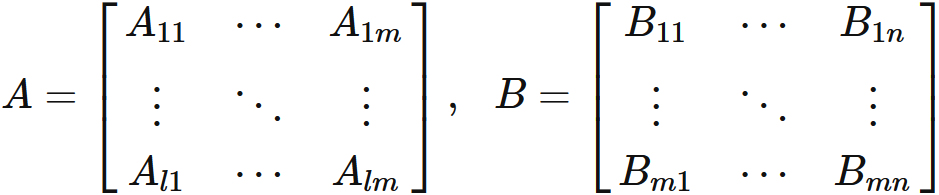 Using the definition of transposed matrix and the definition of product of matrix,
for the $i$-th row, $j$-th column element of $(AB)^T$,
we see that
Using the definition of transposed matrix and the definition of product of matrix,
for the $i$-th row, $j$-th column element of $(AB)^T$,
we see that
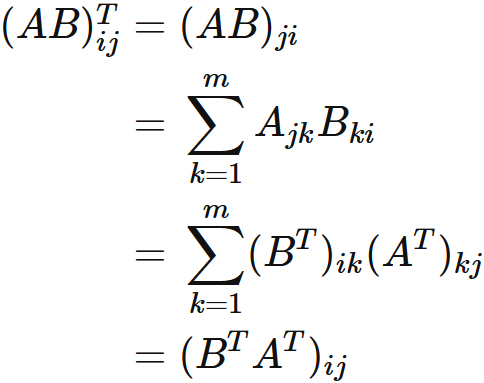 . Since this holds for any element, we obtain
. Since this holds for any element, we obtain
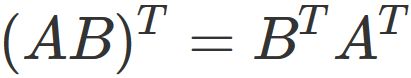 .
.
Let $A$ be a $l \times m$ matrix, and $B$ be a $m \times n$ matrix, written as
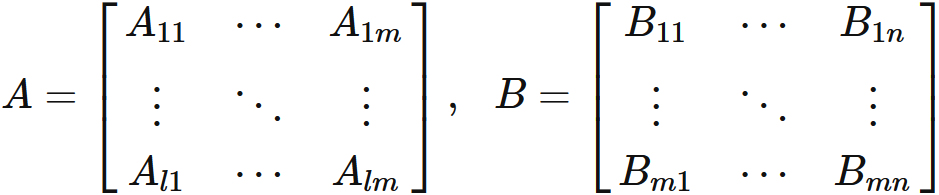
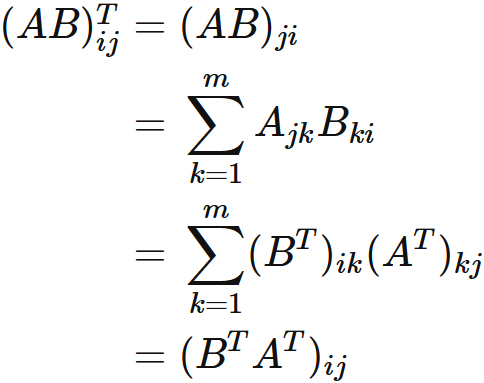
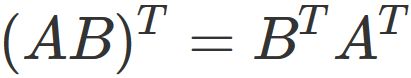
Inverse
If a matrix $A$ is invertible,
the transpose of $A$ is also invertible,
and the inverse matrix of $A^{T}$ is $(A^{-1})^{T}$, that is,

Proof
Let $A$ be an invertible matrix. There exists $A^{-1}$ for which the following holds
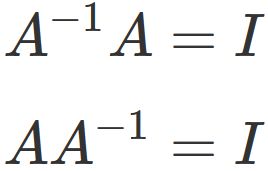 $$
\tag{4.1}
$$
, where $I$ is the identity matrix.
By the propery of transpose of product of two matrices,
and the first equation of $(4.1)$, we see that
$$
\tag{4.1}
$$
, where $I$ is the identity matrix.
By the propery of transpose of product of two matrices,
and the first equation of $(4.1)$, we see that
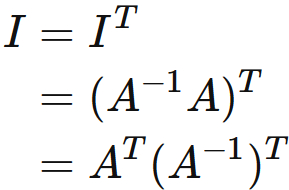 $$
\tag{4.2}
$$
Simimary, by the second equation of $(4.2)$, we see that
$$
\tag{4.2}
$$
Simimary, by the second equation of $(4.2)$, we see that
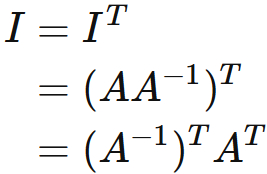 $$
\tag{4.3}
$$
Eq. $(4.2)$ and $(4.3)$ give
$$
\tag{4.3}
$$
Eq. $(4.2)$ and $(4.3)$ give
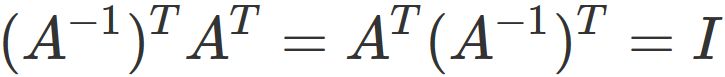 .
This expression shows that $ (A ^ {-1}) ^ {T} $ is the inverse matrix of $ A ^ {T} $, that is,
.
This expression shows that $ (A ^ {-1}) ^ {T} $ is the inverse matrix of $ A ^ {T} $, that is,
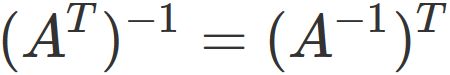 .
.
Let $A$ be an invertible matrix. There exists $A^{-1}$ for which the following holds
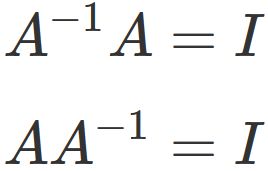
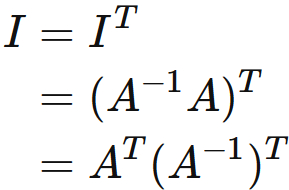
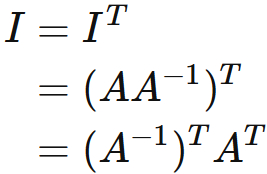
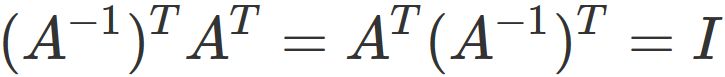
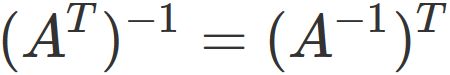
Determinant
Let $A$ be a square matrix,
and $|A^{T}|$
be the determinant of transpose of $A$.
$|A^{T}|$ is equal to the determinant of $A$, that is,
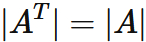
Proof
By definition, the determinant of transpose of an arbitray $n \times n$ matrix $A$ is written as
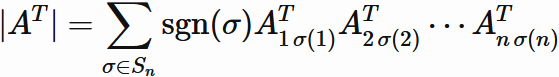 ,
where $\sigma$ denotes a function,
called permutation,
that reorders the set of integers,
$
\{
1,2,\cdots,n
\}
$
$S_{n}$ denotes
the set of all such permutations,
$\mathrm{sgn}(\sigma) $ is
a sign depending on the permutation,
and
a sum $\sum_{\sigma \in S_{n}}$ involves all permutations.
(For details, see "definition of determinant".)
,
where $\sigma$ denotes a function,
called permutation,
that reorders the set of integers,
$
\{
1,2,\cdots,n
\}
$
$S_{n}$ denotes
the set of all such permutations,
$\mathrm{sgn}(\sigma) $ is
a sign depending on the permutation,
and
a sum $\sum_{\sigma \in S_{n}}$ involves all permutations.
(For details, see "definition of determinant".)
Since $ A_ {ij} ^ {T} = A_ {ji} $ from the definition of transpose,
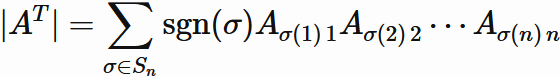 .
The permutation is bijective.
Therefore,
for an arbitray permutation $ \sigma $,
there exists an inverse map $ \sigma^{-1} $
such that
.
The permutation is bijective.
Therefore,
for an arbitray permutation $ \sigma $,
there exists an inverse map $ \sigma^{-1} $
such that
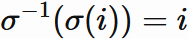 , where $i=1,2,\cdots,n$.
Using this, we have
, where $i=1,2,\cdots,n$.
Using this, we have
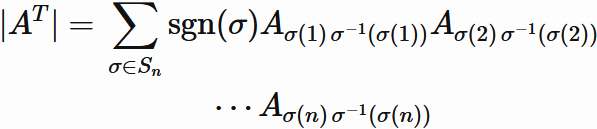 $$
\tag{5.1}
$$
.
Since $\sigma$
is a map that maps
$ \{1,2, \cdots, n \}$
to the same set
$ \{1,2, \cdots, n \}$,
there exists $j$ $(j=1,\cdots,n)$
such that $\sigma(j) = 1$.
Therefore $(5.1)$ can be written as
$$
\tag{5.1}
$$
.
Since $\sigma$
is a map that maps
$ \{1,2, \cdots, n \}$
to the same set
$ \{1,2, \cdots, n \}$,
there exists $j$ $(j=1,\cdots,n)$
such that $\sigma(j) = 1$.
Therefore $(5.1)$ can be written as
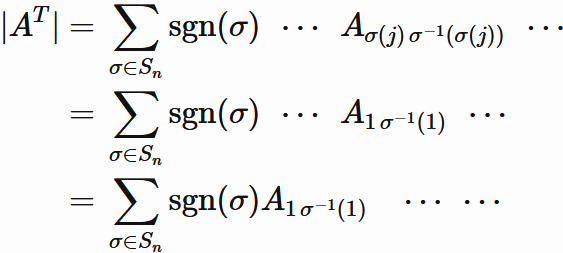 , where
,in the last line,
the order of multiplication is just changed.
Similary,
there exists $k$ $(k=1,\cdots,n, k\neq j)$
such that $\sigma(k) = 2$.
We see that
, where
,in the last line,
the order of multiplication is just changed.
Similary,
there exists $k$ $(k=1,\cdots,n, k\neq j)$
such that $\sigma(k) = 2$.
We see that
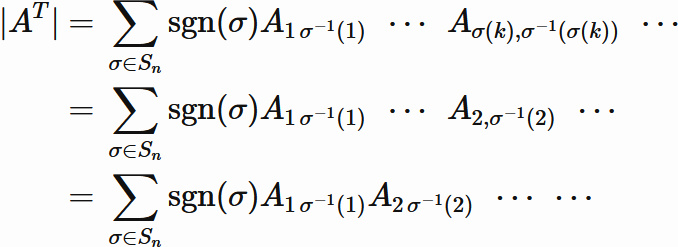 By repeating the same procedure to the end,
we obtain
By repeating the same procedure to the end,
we obtain
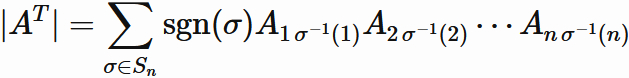 $$
\tag{5.2}
$$
Since $\sigma^{-1}$ of an even permutation $\sigma$
is also an even permutation,
and $\sigma^{-1}$ of an odd permutation $\sigma$ is also an odd permutation,
$\mathrm{sgn}(\sigma^{-1}) = \mathrm{sgn}(\sigma)$ holds.
Therefore, we can write
$$
\tag{5.2}
$$
Since $\sigma^{-1}$ of an even permutation $\sigma$
is also an even permutation,
and $\sigma^{-1}$ of an odd permutation $\sigma$ is also an odd permutation,
$\mathrm{sgn}(\sigma^{-1}) = \mathrm{sgn}(\sigma)$ holds.
Therefore, we can write
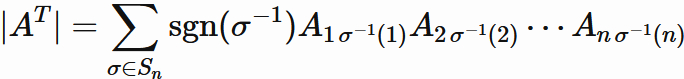 $\sigma$
is a map that maps
$ \{1,2, \cdots, n \}$
to the same set
$ \{1,2, \cdots, n \}$,
and similary,
$\sigma^{-1}$
is a map that maps
$ \{1,2, \cdots, n \}$
to the same set
$ \{1,2, \cdots, n \}$.
The set of
all $ \sigma^{-1}$
is the same as the set of
all $\sigma$,
Therefore, in Eq.$(5.2)$,
$ \sum_{\sigma \in S_{n}}$
can be replaced with
$\sum_{\sigma^{-1} \in S_{n}}$
$\sigma$
is a map that maps
$ \{1,2, \cdots, n \}$
to the same set
$ \{1,2, \cdots, n \}$,
and similary,
$\sigma^{-1}$
is a map that maps
$ \{1,2, \cdots, n \}$
to the same set
$ \{1,2, \cdots, n \}$.
The set of
all $ \sigma^{-1}$
is the same as the set of
all $\sigma$,
Therefore, in Eq.$(5.2)$,
$ \sum_{\sigma \in S_{n}}$
can be replaced with
$\sum_{\sigma^{-1} \in S_{n}}$
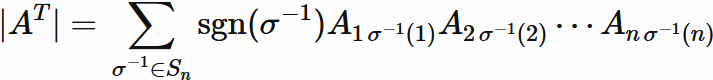 Since $\sigma^{-1}$ is one of permutation,
we can rewrite $\sigma^{-1}$ as $\xi \hspace{1mm} (\in S_{n})$,
Since $\sigma^{-1}$ is one of permutation,
we can rewrite $\sigma^{-1}$ as $\xi \hspace{1mm} (\in S_{n})$,
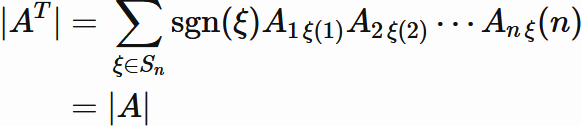 In this way,
the determinant of transpose of a square matrix is equal to the determinant of the square matrix.
In this way,
the determinant of transpose of a square matrix is equal to the determinant of the square matrix.
By definition, the determinant of transpose of an arbitray $n \times n$ matrix $A$ is written as
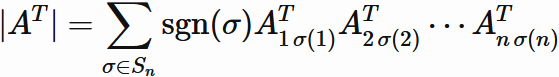
Since $ A_ {ij} ^ {T} = A_ {ji} $ from the definition of transpose,
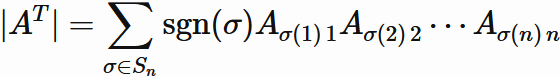
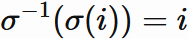
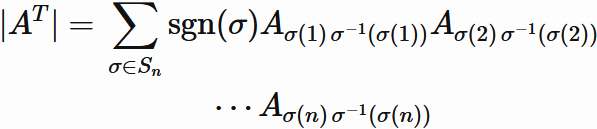
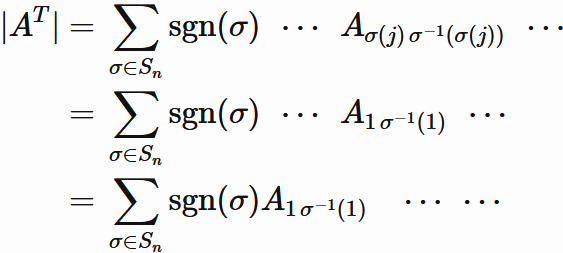
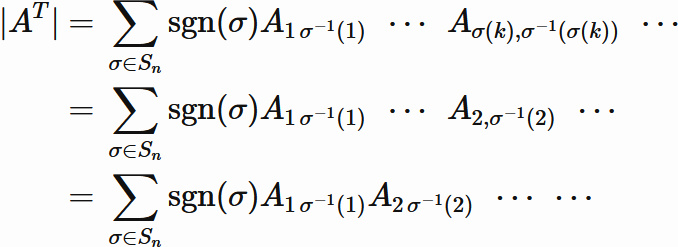
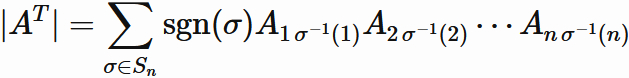
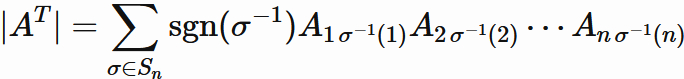
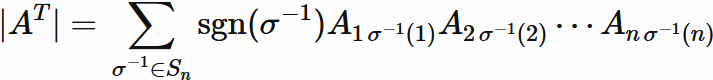
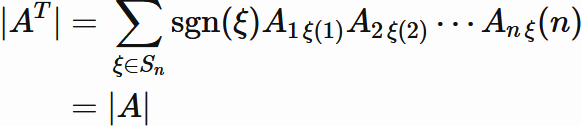
Trace
Let $A$ a squared matrix and $ A ^ {T} $ be the transpose of $A$.
The trace of $A^{T}$ is equal to the trace of $ A $:
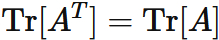
Proof
Let $A$ an $n \times n$ matrix, and $A_{ij}$ be the $i$-th row, $j$-th column element of $A$. By the definition of transpose, we have
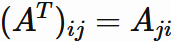 , whrere ($i,j=1,2 \cdots , n$).
This and the defintion of the trace give
, whrere ($i,j=1,2 \cdots , n$).
This and the defintion of the trace give
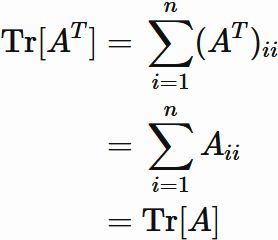
Let $A$ an $n \times n$ matrix, and $A_{ij}$ be the $i$-th row, $j$-th column element of $A$. By the definition of transpose, we have
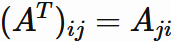
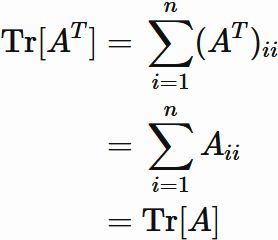
Linearity
Let $A$ and $B$ be $m \times n$ matrices and alpha be a scalar.
The transpse is a linear transformation:
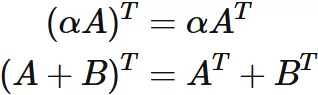
Proof
Suppose $A$ and $B$ are represented as
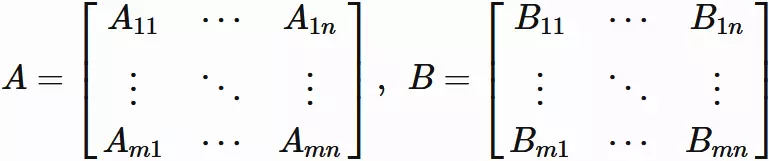 Then
Then
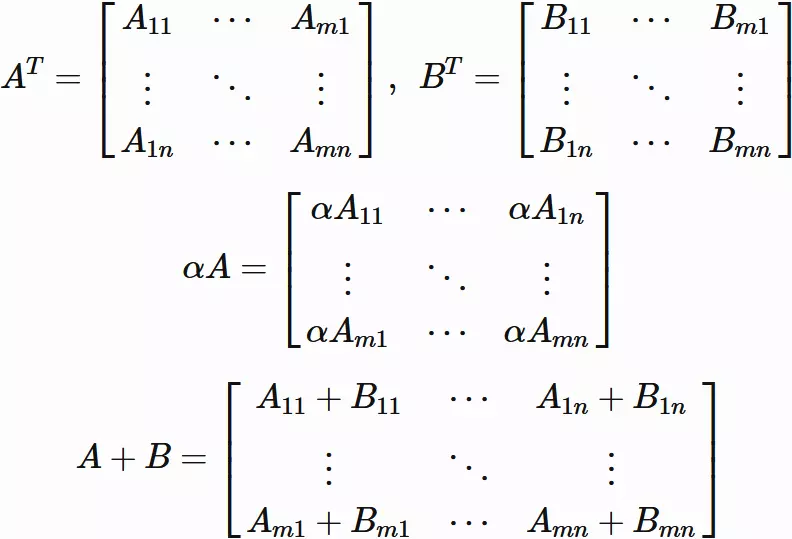 We see that
We see that
 and
and

Suppose $A$ and $B$ are represented as