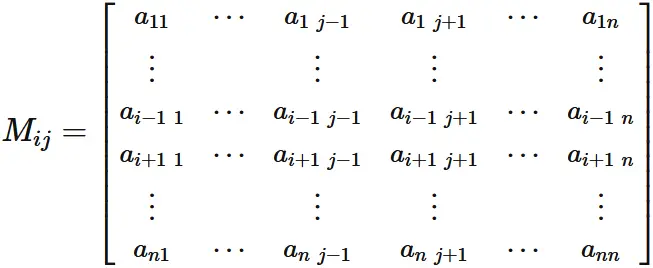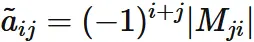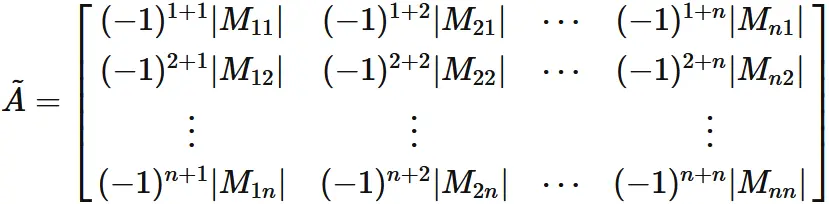Cofactor Matrix (examples)
| Examples | |
|---|---|
| - | Ex: $2 \times 2$ matrix |
| - | Ex: $3 \times 3$ matrix |
| - | Ex: $4 \times 4$ matrix |
| General | |
|---|---|
| - | Definition |
Example: $2 \times 2$ matrix
Let $A$ be a $2 \times 2$ matrix defined as
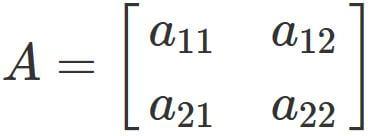
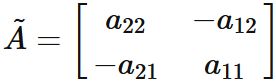
Answer
Let $M_{ij}$ be a submatrix given by removing $i$-th row and $j$-th column from $A$,
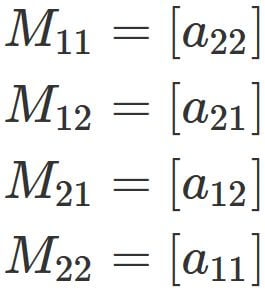The determinant of $M_{ij}$ is
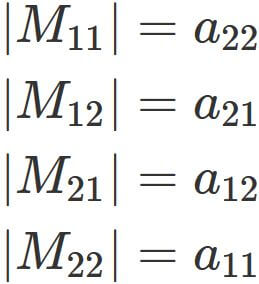Each element of the cofactor matrix is defined as
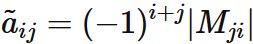Specifically, we see that
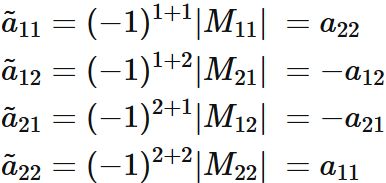and in the form of a matrix,
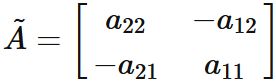
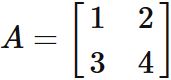Each element of $\tilde{A}$ is
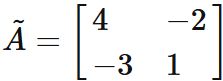
Matrix $A$
Cofactor Matrix $\tilde{A}$
Let $M_{ij}$ be a submatrix given by removing $i$-th row and $j$-th column from $A$,
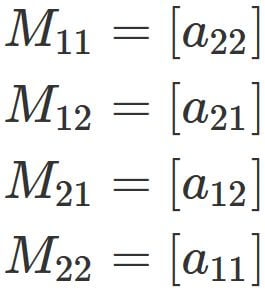
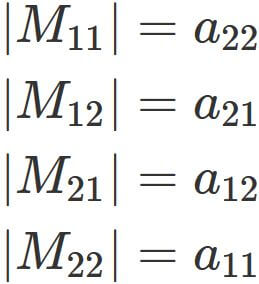
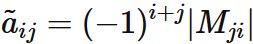
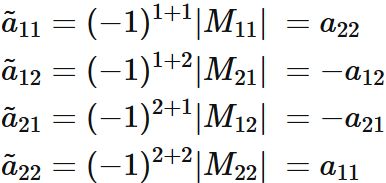
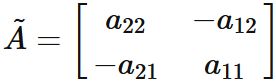
Example
Let $A$ be a $2 \times 2$ matrix given as
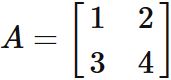
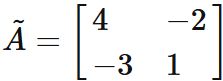
Calculator
Enter a $2 \times 2$ matrix and press "Execute" button.
Its cofactor matrix is displayed.
Matrix $A$
| 1 | 2 | |
| 1 | ||
| 2 |
Example: $3 \times 3$ matrix
Let $A$ be a $3 \times 3$ matrix given as
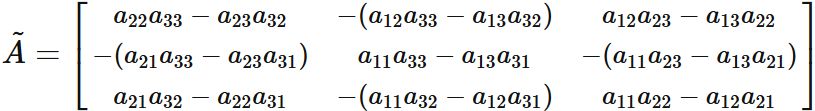
Answer
Let $M_{ij}$ be a submatrix given by removing $i$-th row and $j$-th column from $A$,
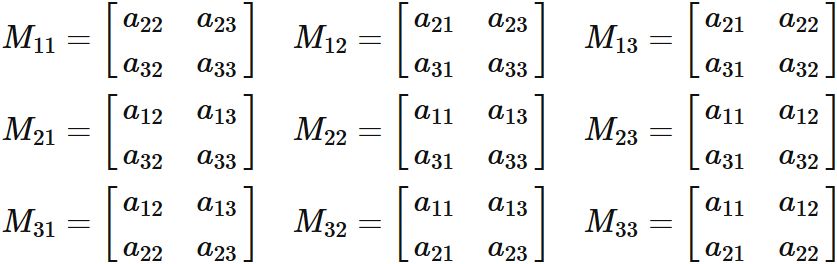The determinant of $M_{ij}$ is
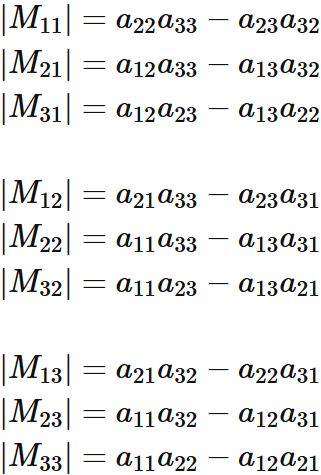Each element of the cofactor matrix $\tilde{A}$ is defined as
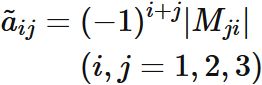Specifically, we see that
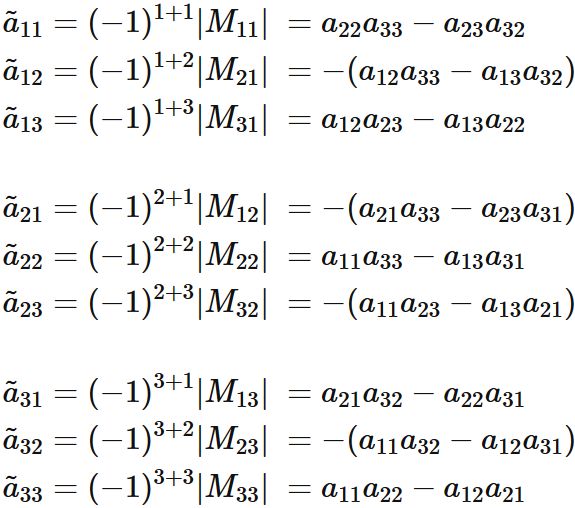and in the form of a matrix,
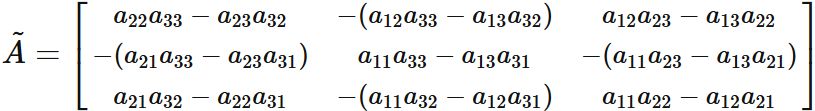
Let $A$ be a 3x3 matrix given as
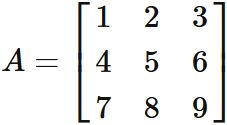Each element of $\tilde{A}$ is
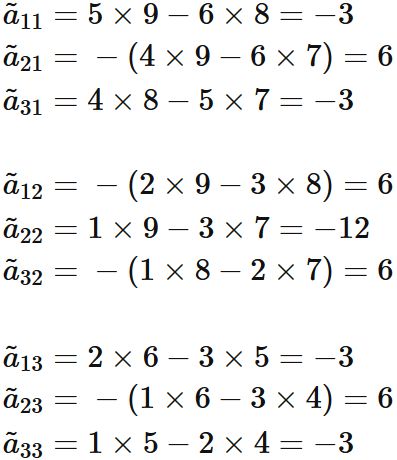and in the form of a matrix,
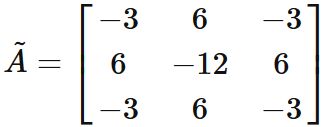
Let $M_{ij}$ be a submatrix given by removing $i$-th row and $j$-th column from $A$,
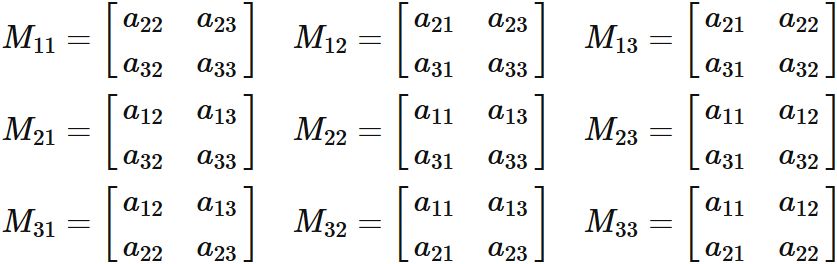
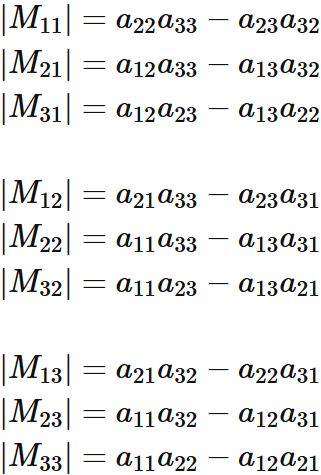
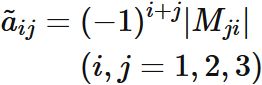
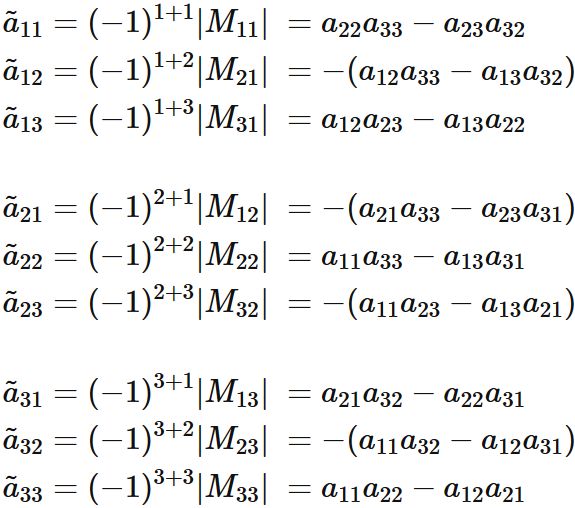
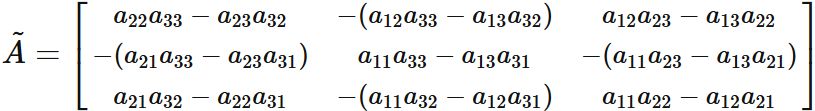
Example:
Let $A$ be a 3x3 matrix given as
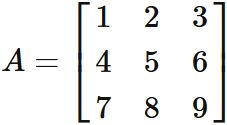
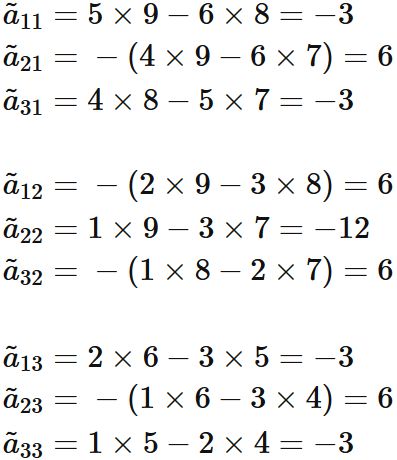
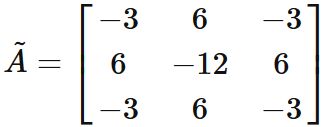
Calculator
Enter a $3 \times 3$ matrix and press "Execute" button.
Its cofactor matrix is displayed.
Example: $4 \times 4$ matrix
Find the cofactor matrix of
Answer
Let $M_{ij}$ be a submatrix given by removing $i$-th row and $j$-th column from $A$,
The determinant of $M_{ij}$ is respectively
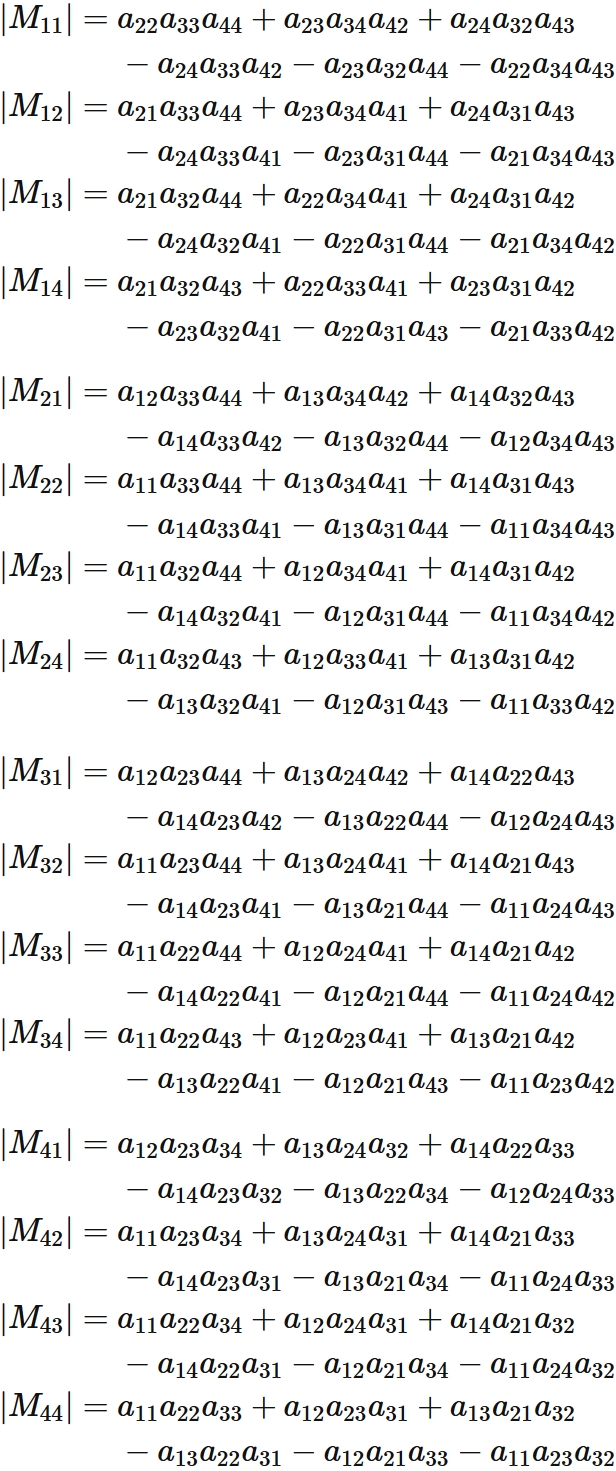(See 3x3 determinant).
Each element of the cofactor matrix $\tilde{A}$ is defined as
$$
\tilde{a}_{ij} = (-1)^{i+j}|M_{ji}|
$$
Specifically, we see that
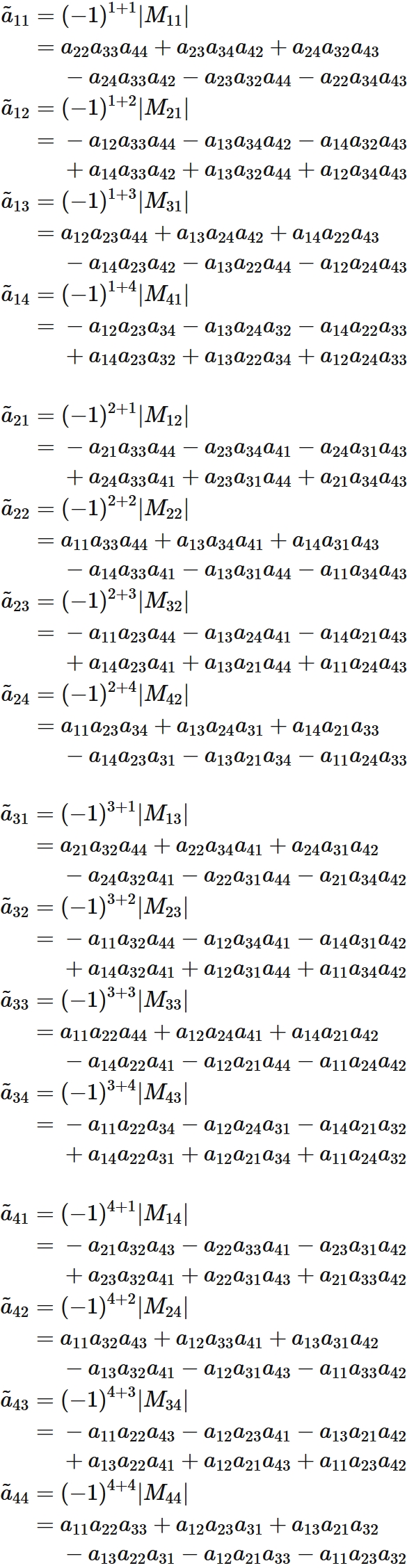
Let $M_{ij}$ be a submatrix given by removing $i$-th row and $j$-th column from $A$,
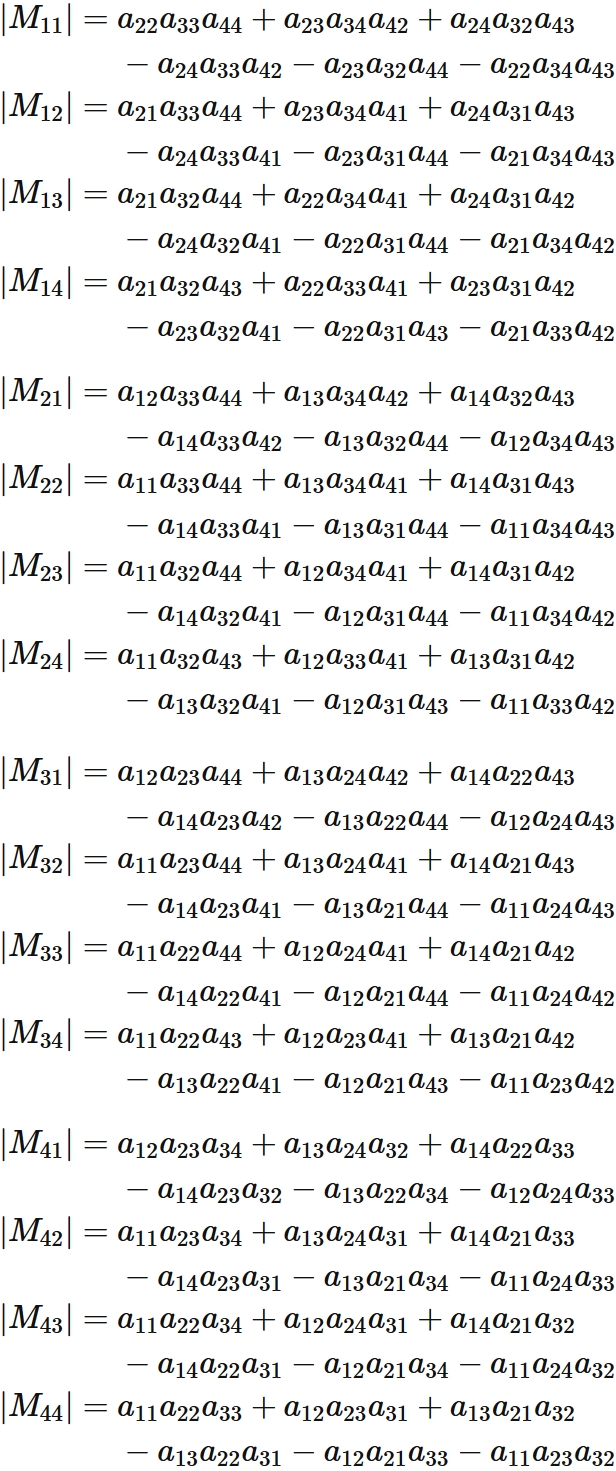
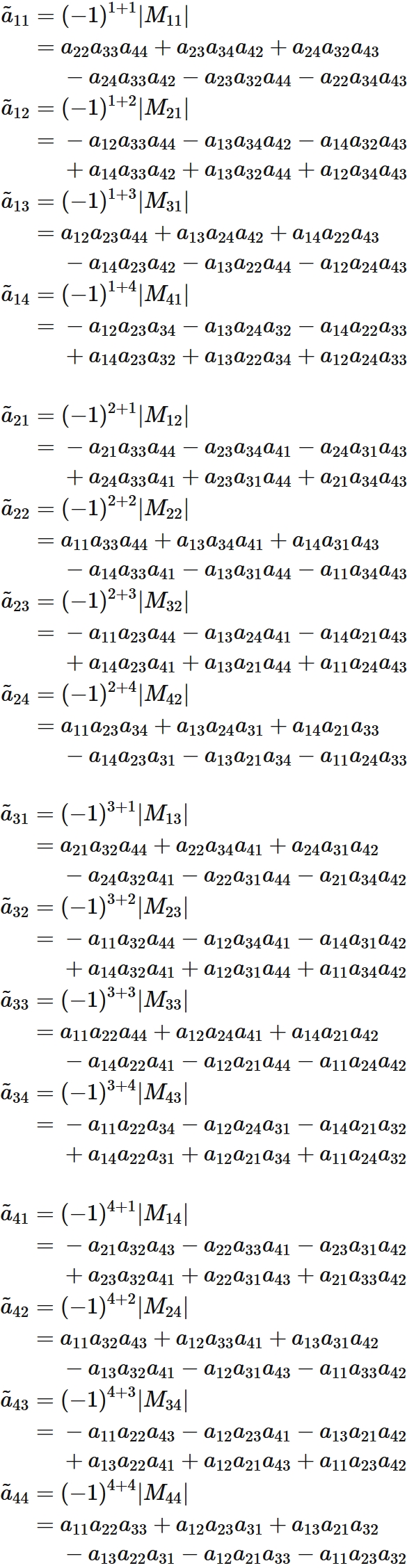
Calculator
Enter a $4 \times 4$ matrix and press "Execute" button.
Its cofactor matrix is displayed.
Definition of cofactor matrix
Let $a_{ij}$ be the $i$-th row and $j$-th column element of an $n \times n$ matrix $A$,
and $M_{ij}$ be the sub-matrix obtained by removing the $i$-th row and $j$-column:
