How to find the inverse matrix of a 4x4 matrix
Find the inverse of

Answer
There are mainly two ways to obtain the inverse matrix. One is to use Gauss-Jordan elimination and the other is to use the adjugate matrix. We employ the latter, here.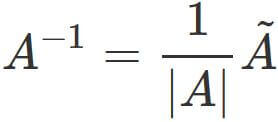
The determinant of $A$ can be obtained by using the cofactor expansion. The cofactor expansion along the first column is
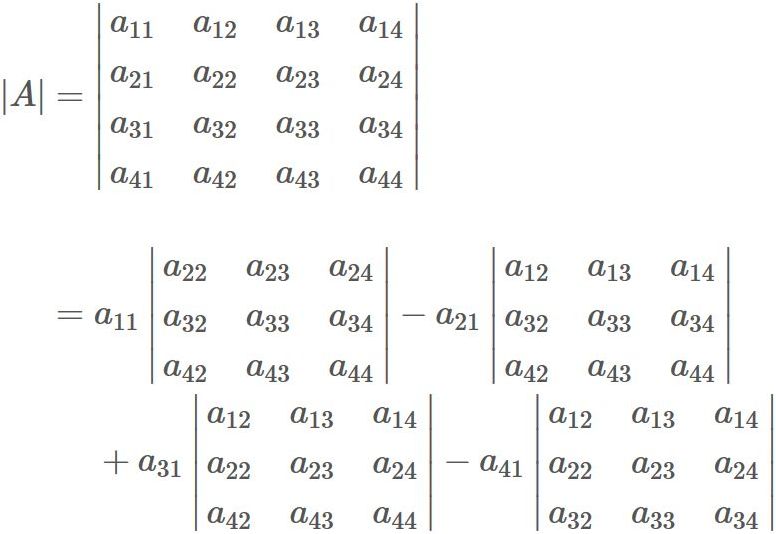


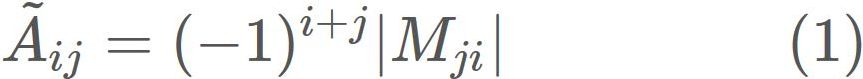
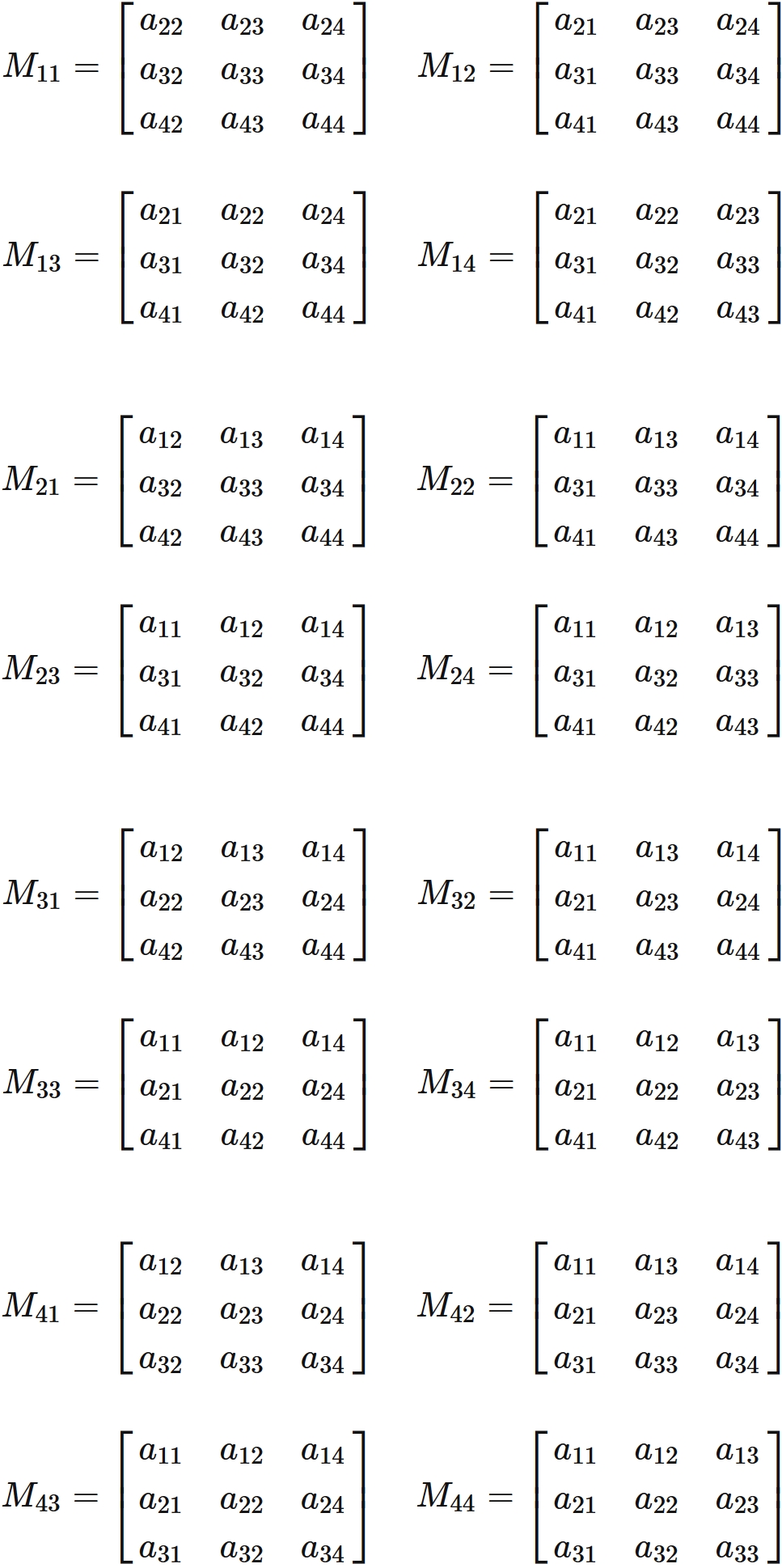
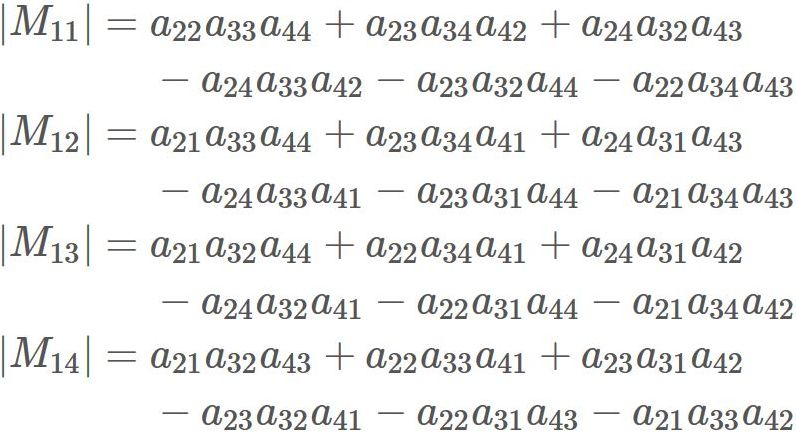
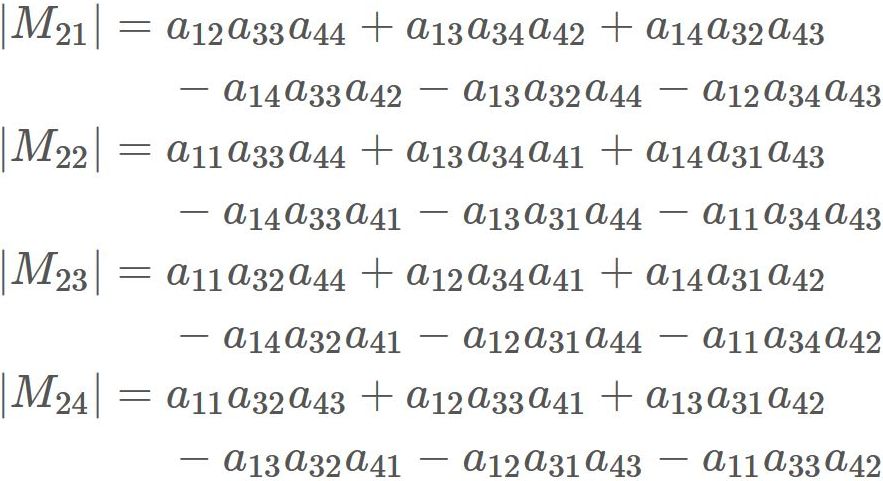
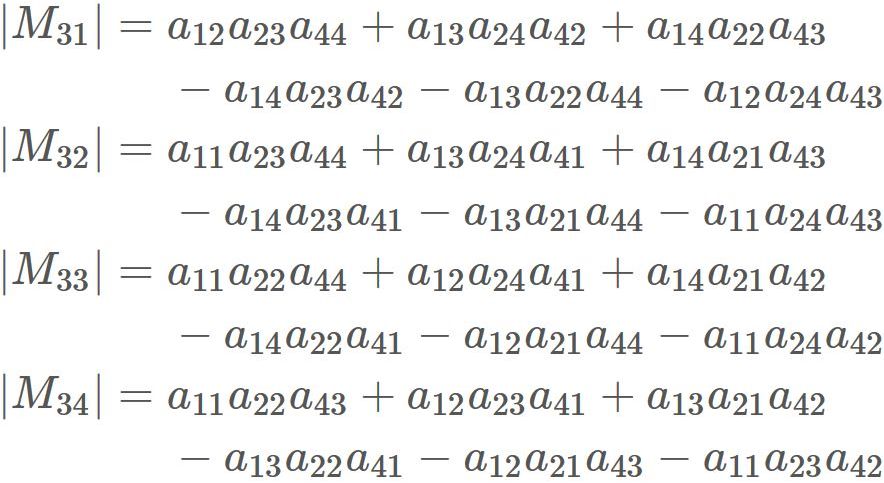
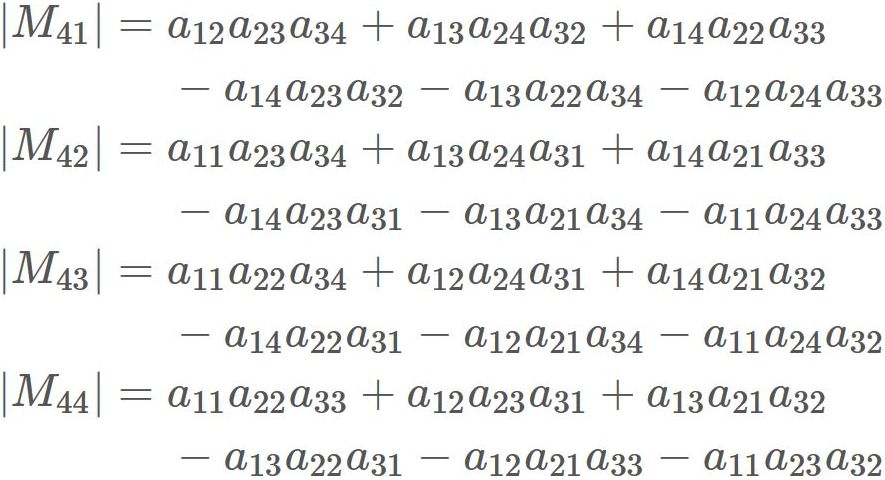
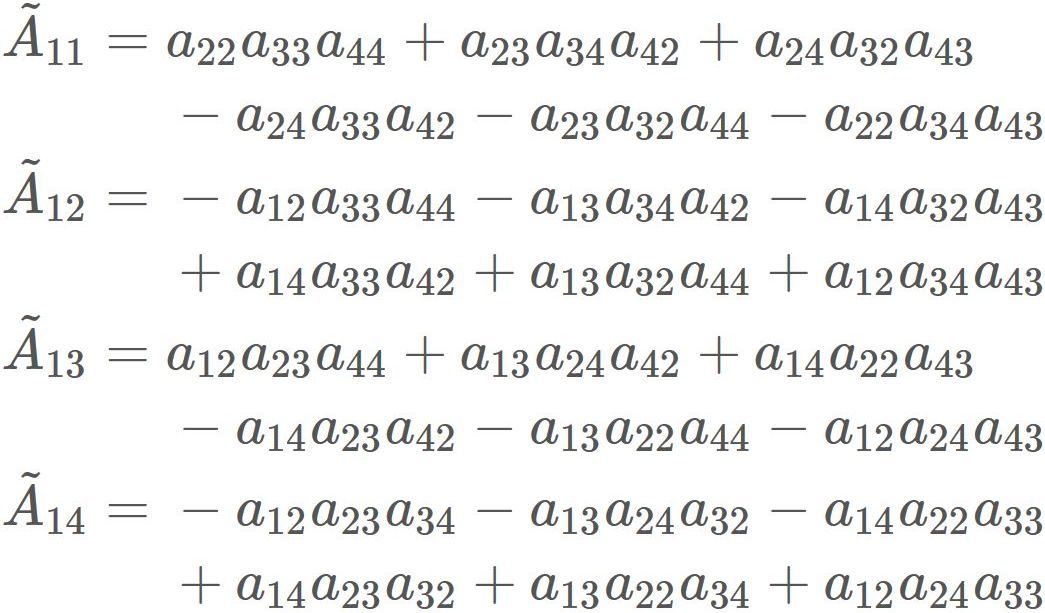
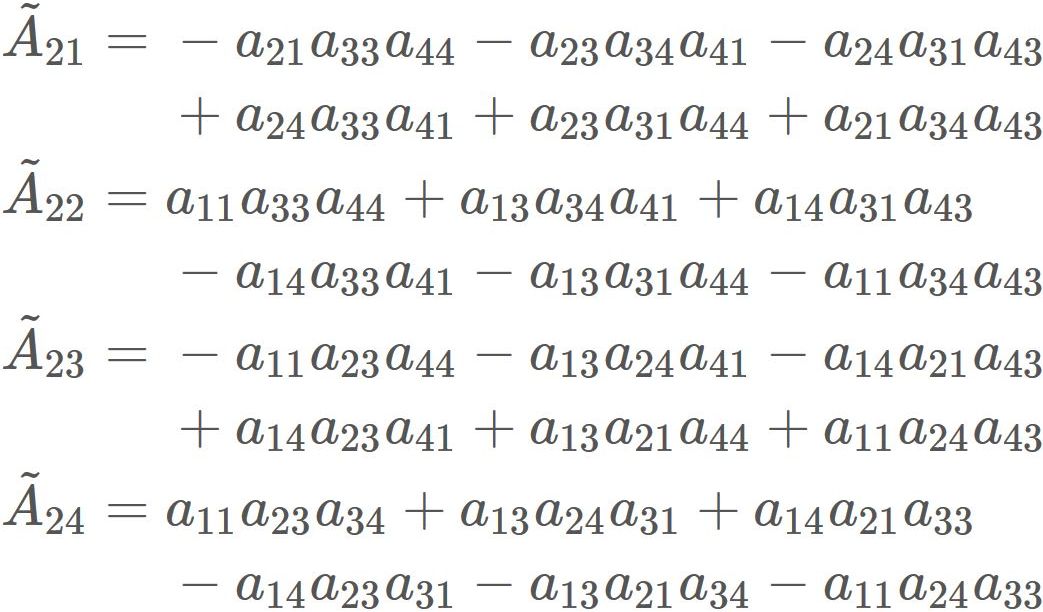
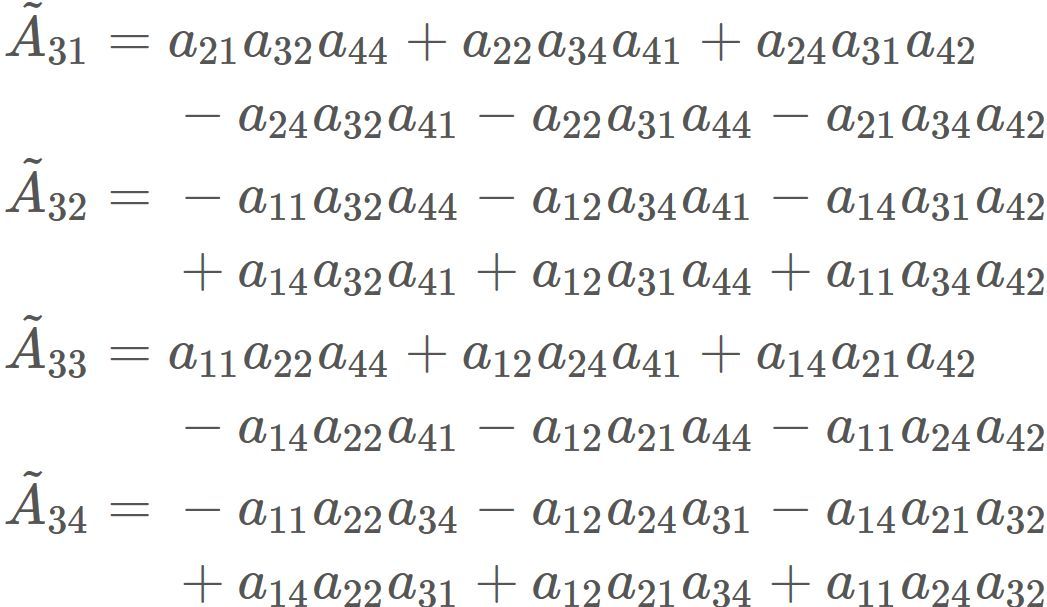
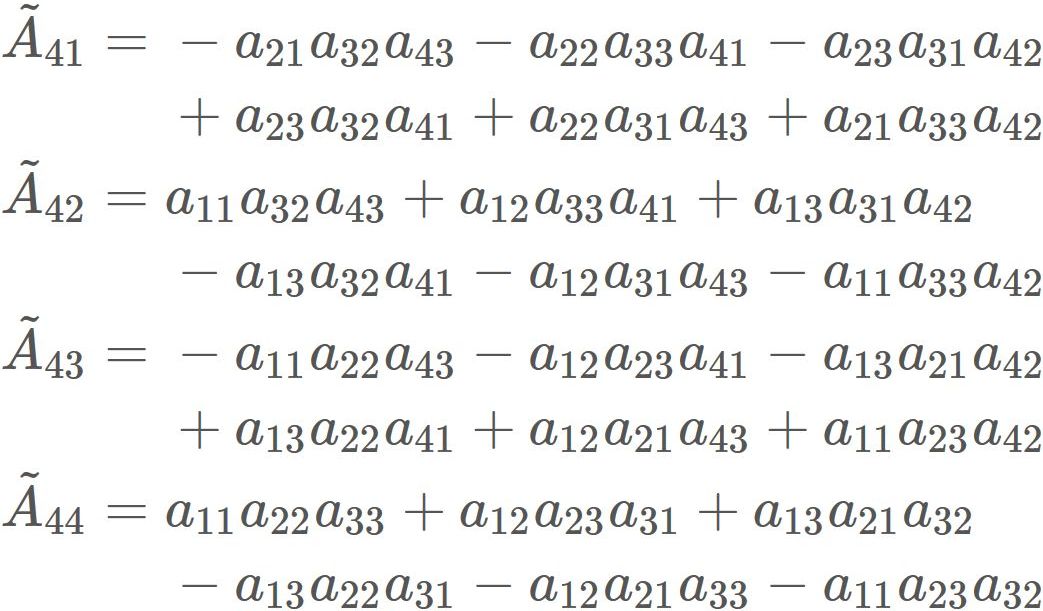
We have found $|A|$ and $\tilde{A}$. Therefore, substituting them into
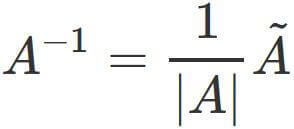
Find the inverse of
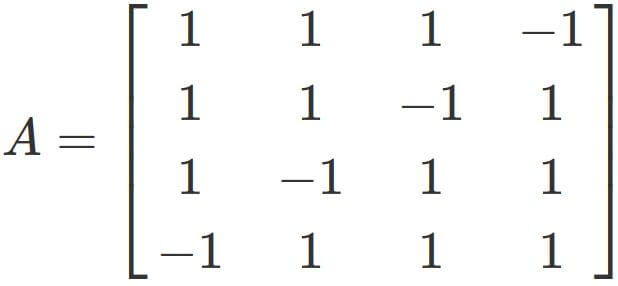
The determinant of $A$ is
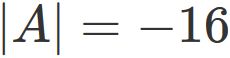
The submatrices of $A$ are
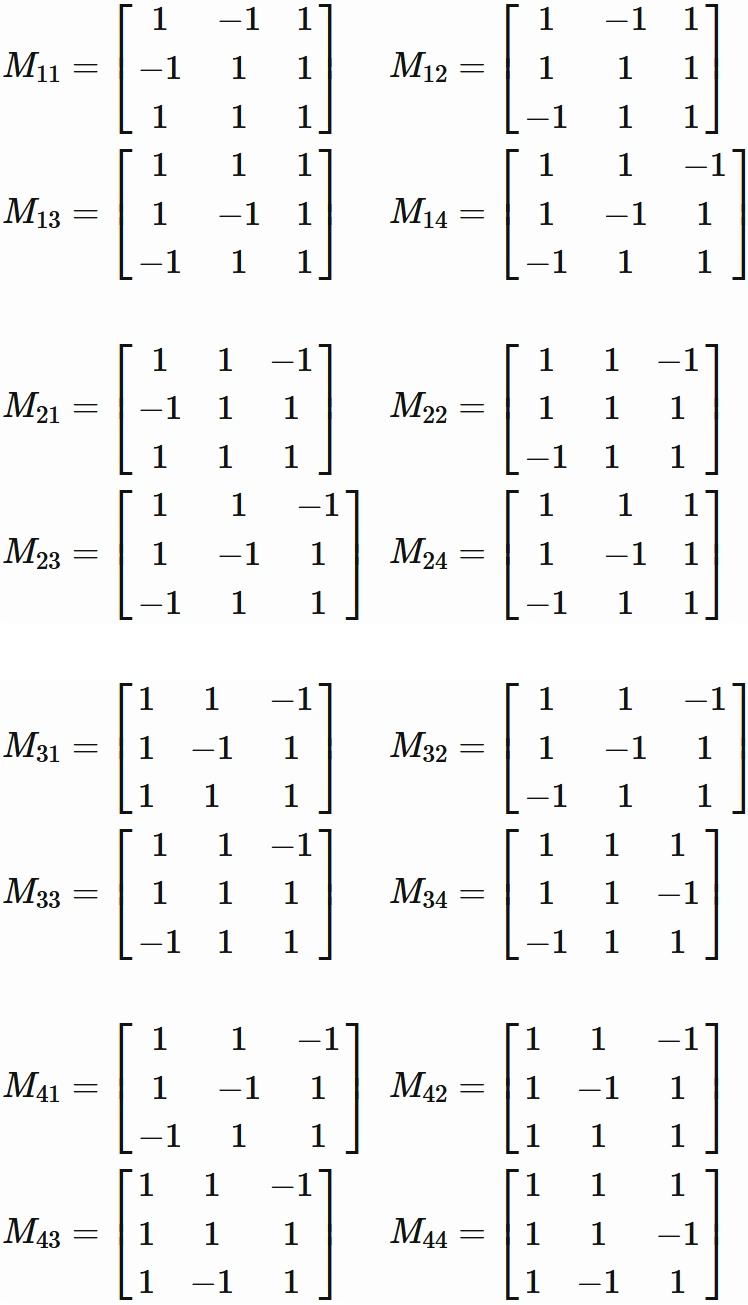
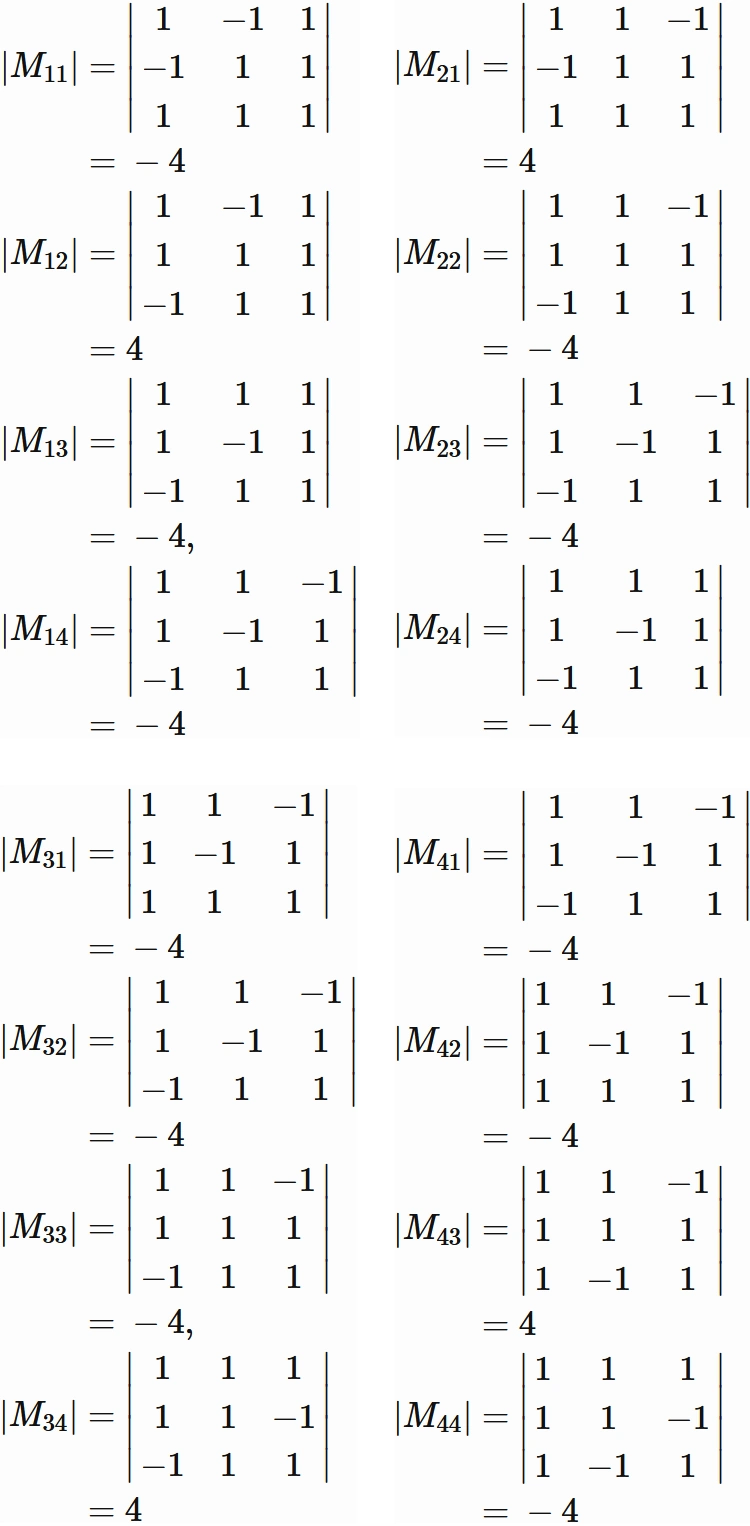
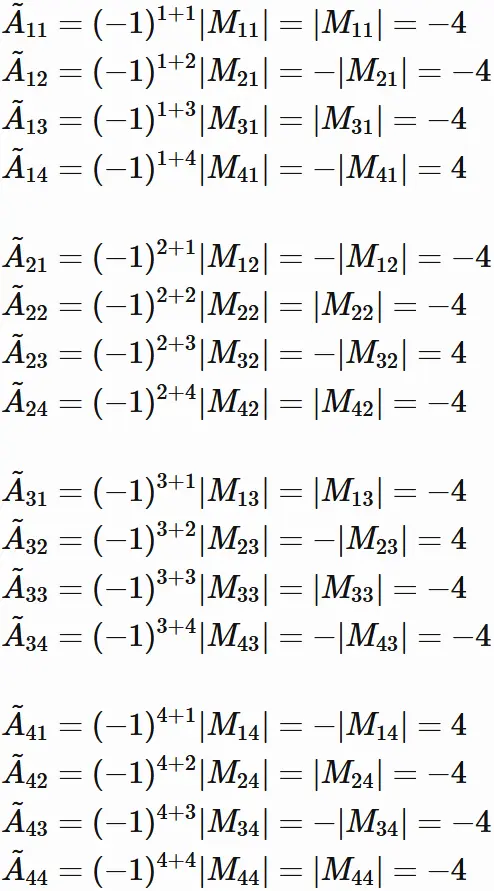
Therefore, $A^{-1}$ is
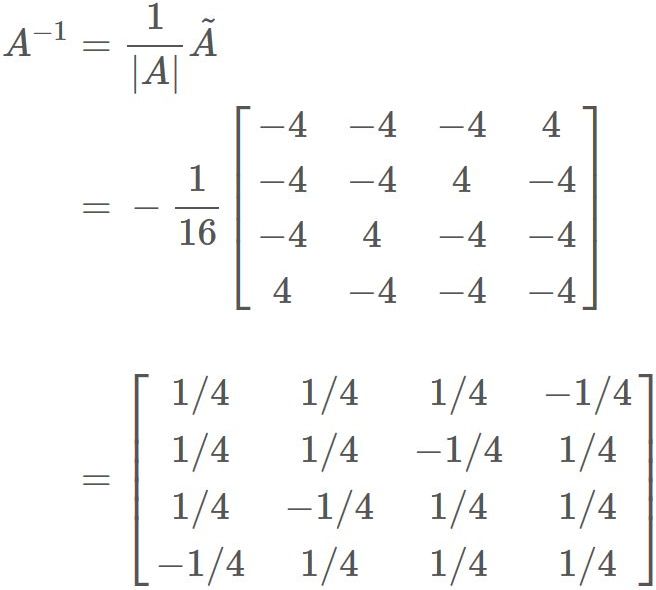
Calculator
Enter a 4x4 matrix and press "execute button". The inverse matrix is displayed.
Matrix
Inverse matrix
| 1 | 2 | 3 | 4 | |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |